التكافؤ العاملي لمقياس جودة الحياة في ضوء طريقة معالجة القيم المفقودة

تنزيل الملف

 

 

د. علاء محمد علي البنوي¹

1 باحث في القياس والتقويم التربوي، جامعة اليرموك

بريد الكتروني: haiytham.zreqat@gmail.com

HNSJ, 2021, 2(10); https://doi.org/10.53796/hnsj2103

 

تاريخ النشر: 01/10/2021م تاريخ القبول: 09/09/2021م

المستخلص

هدفت هذه الدراسة لتقصي أثر طريقة تعويض القيم المفقودة (الوسط الحسابي، نقطة الاتجاه الخطية، القيمة التقريبية) على بناء مقياس جودة الحياة المطبق على طلبة الجامعات الأردنية في دراسة الشوبكي(2021) ولتحقيق أهداف الدراسة تم إجراء فقد عشوائي بنسبة (10%) من البيانات المستخدمة في نفس الدراسة. ثم تم تعويض بدل القيم المفقودة بثلاث طرق. وخلصت الدراسة لأن الطرق الثلاث فعّالة في تعويض القيم والمحافظة على البناء العاملي للمقياس والحصول على بيانات تحقق جميع أنواع التكافؤ (الشكلي، المتري، القياسي، البواقي) مع بيانات المقياس الأصلي.

الكلمات المفتاحية: التكافؤ العاملي، جودة الحياة، القيم المفقودة

 

Research Article

Invariance of the Quality-of-Life Scale According to Missing Values Handling Methods.

Dr. Alaa Mohammed Ali Al Banwi ¹

¹ Researcher in educational measurement and evaluation, Yarmouk University

Email: haiytham.zreqat@gmail.com

HNSJ, 2021, 2(10); https://doi.org/10.53796/hnsj2103

 

Published at 01/10/2021 Accepted at 09/09/2021

Abstract

This study aimed to investigate the effect of the method of compensating for missing values ​​(arithmetic mean, linear trend point, approximate value) on building a measure of the quality of life applied to Jordanian university students in the Al-Shobaki study (2021). Used in the same study. The allowance for missing values ​​was then made up in three ways. The study concluded that the three methods are effective in compensating the values ​​and maintaining the factorial construction of the scale and obtaining data that achieve all types of equivalence (formal, metric, and standard, residual) with the original scale data.

 

Key Words: factor equivalence, quality of life, missing values.

 

المقدمة:

في ضوء التطور الكبير الواسع في مجال البحث العلمي كان لابد من تطوير الأدوات المستخدمة لتحقيق أهداف البحث العلمي ولعل المقاييس والاختبارات تعد أهم الوسائل والأدوات المستخدمة في العلوم الإنسانية والتربوية.

ويتم تطبيق المقاييس بشكل مباشر على الأفراد وبأشكال مختلفة أهمها الأوراق المطبوعة وحديثا الشكل الإلكتروني ومن اهم المشاكل التي تواجه تطبيق المقاييس بشكلها الورقي والإلكتروني عدم استجابة الفرد لجميع فقرات المقياس مما يشكل تحديا أمام الباحث فمن جهة إن الاستجابات الناقصة تشكل معلومات مفقودة غير موجودة ويمكن أن تشير لما يظلل البحث وبخاصة خصائص المقياس السيكومترية التي تتطلب دقة عالية ومن جهة أخرى فان الاستجابات على تلك المقاييس يتم تفريغها رقميا في جداول الكترونية ليتم بعد ذلك إجراء بعض الحسابات الخاصة ببعض الاختبارات الإحصائية تمهيدا للإجابة عن أسئلة الدراسة وفحص فرضياتها وبوجود بعض الفقرات الغير مجاب عليها يتكون ما يسمى بالقيم المفقودة (missing values) في مصفوفة البيانات مما يعرقل حساب قيم بعض الاختبارات الإحصائية وإجراء بعض الحسابات حيث أن بعض الاختبارات الإحصائية تتطلب وجود مصفوفة بيانات مكتملة غير ناقصة (Allison, 2002).

وقد بحث العلماء في طرق عديدة لجعل مصفوفة البيانات مكتملة وقابلة للتحليل حيث ظهر عدد من الطرق يتجه بعضها لحذف استجابات الفرد على جميع الفقرات عند وجود عدم استجابة على أي من الفقرات ولكن لعدم عمليه هذه الطريقة والحرص على عدم ضياع البيانات اتجهت بعض الطرق الأخرى لعلاج القيم المفقودة من خلال تعويض قيم مكانها ومن تلك الطرق (الوسط الحسابي (Mean)، نقطة الاتجاه الخطي (linear Trend Point)، التقريب الخطي (Linear Interpolation))، حيث تعتمد طريقة الوسط الحسابي على تعويض قيمة الوسط الحسابي للقيم الموجودة بدلا من القيم المفقودة على مستوى المتغير الواحد (الفقرة)، بينما تهتم طريقة نقطة الاتجاه بتعويض نقطة تعزز الاتجاه الذي تسير البيانات باتجاهه من خلال التنبؤ بقيمة تلك النقطة على اعتبار أننا نتعامل مع انحدار، وكذلك فان طريقة القيم التقريبية تعوض بدلا من القيم المفقودة قيم يتم تقريبها على مستوى المتغير باستخدام القيمتين المجاورتين للقيمة المفقودة (Royston, 2005).

وقد اهتمت الدراسات بشكل أكبر بالطرق الثلاث (الوسط الحسابي، نقطة الاتجاه الخطي، التقريب الخطي) وكذلك فان باحثين قاموا بدراسة أثر طريقه علاج القيم المفقودة على الخصائص السيكومترية للاختبار وغيرها مثل دراسة كوكلوك وكاري (cokluk & kayri, 2011) ودراسة ويكيل (Wickhel, 2014).

الدراسات السابقة:

أجرى كوكلوك وكاري (cokluk & kayri, 2011) دراسة هدف لتقصي أثر طرق علاج القيم المفقودة على صدق وثبات المقاييس، حيث تم مقارنة معاملات الارتباط المصححة ومعاملات الاتساق الداخلي كرونباخ-الفا التي الحصول عليها بعد معالجة القيم المفقودة بطرق مختلفة، لبيانات تم الحصول من خلال تطبيق مقياس القدرية (Sekercioglu, 2008) على 200 من المعلمين، وقد أظهرت النتائج عدم اختلاف بناء العامل الواحد باختلاف طريقة علاج القيم المفقودة، بينما انخفضت قيم معاملات الثبات والاتساق الداخلي باستخدام البيانات المعالجة.

وكذلك أجري ويفر وماكسويل (Weaver & Maxwell, 2014) دراسة هدفت لتحديد أفضل طريقة للتعامل مع القيم المفقودة من خلال إجراء تحليل عاملي استكشافي وعاملي توكيدي من خلال برمجية (SPSS) حيث تبين أن أفضل طريقة للتعامل مع القيم المفقودة هي استخدام مصفوفة التباينات لتعظيم التوقعات كمدخلات للتحليل.

كما أجري الصرايرة (2018) دراسة محاكاة لتقصي أثر نسبة القيم المفقودة وطريقة معالجتها في تقدير القيمة القصوى لدالة معلوماتية الفقرة ومؤشر ثباتها، من خلال توليد بيانات افتراضية باستخدام برمجية (WINGEN3) لاستجابات (1000) مفحوص على (50) فقرة تتبع النموذج ثلاثي المعلمة (3PLM) وبنسب فقد مختلفة (5%، 10%، 15%) باستخدام برمجية اكسيل (EXCEL)، وأظهرت نتائج الدراسة وجود فروق في دقة تقدير القيمة القصوى لدالة معلوماتية الفقرة تعزى للكل من طريقة معالجة القيم المفقودة ونسبة القيم المفقودة والتفاعل بينهما.

وأجرى العناتي، اللبدي والمقصقص (2018) دراسة هدفت للمقارنة بين ثلاث من طرق تعويض القيم المفقودة في الاختبارات العامة وهي الوسط الحسابي، والسطح الساخن، والانحدار من خلال تطبيق اختبارات عامة للرياضيات (MCQ30) على عينة عشوائية من طلبة الصف العاشر حجمها (2100) ثم إجراء حذف عشوائي بنسبة (10%) من الاستجابات، ثم استخدام الطرق الثلاث لتعويض الفقد في البيانات وأظهرت نتائج الدراسة أن الطرق مرتبة حسب الدقة في تقدير معالم الفقرات هي: الانحدار، الوسط الحسابي، السطح الساخن.

مشكلة الدراسة وأسئلتها:

يهتم البحث العلمي باستخدام أدوات قياس دقيقه وصادقه من حيث محتواها وبناؤها وان استخدام الطريقة الغير مناسبه لعلاج القيم المفقودة قد يتسبب في خفض مستوى مصداقيه أو التقليل من مصداقيه أداه الدراسة وقد يتسبب في استبعادها في مراحل العينة الاستطلاعية عدا عن النتائج المضللة للاختبارات الإحصائية في مراحل العينة الرئيسية وتأتي هذه الدراسة للبحث في احدى الخصائص السيكومتريه للمقاييس عند استخدام طرق مختلفة لتعويض القيم المفقودة وهي تحديدا تجيب عن السؤال التالي:

“هل يختلف البناء العاملي لمقياس جودة الحياة باختلاف طريقة تعويض القيم المفقودة (الوسط الحسابي، نقطة الاتجاه الخطي، التقريب الخطي)؟”

أهمية الدراسة:

تكمن أهمية الدراسة النظرية في أنها تزود الأدب النظري المتعلق بالقيم المفقودة في مفاضله بين طرق تعويض القيم المفقودة لتحقيق الصدق العاملي لأداه الدراسة وعمليا فان هذه الدراسة ستوجه الباحثين ومستخدمي المقاييس للطريقة الأنسب لعلاج القيم المفقودة كسبيل للحفاظ على موثوقية أداة الدراسة وخصائصها السيكومتريه.

الإجراءات:

أولا: تم اختيار مقياس جوده الحياة المستخدم في دراسة الشوبكي (2021)، والاكتفاء بما تم التحقق منه من الثبات والصدق الظاهري.

ثانيا: الحصول على البيانات التي تم جمعها في دراسة الشوبكي (2021)، والمطبقة على طلبه جامعه اليرموك.

ثالثا: إجراء فقد عشوائي بنسبه 10% من البيانات المجموعة في الخطوة السابقة من خلال برمجية اكسيل.

رابعا: تم علاج القيم المفقودة التعويض من بدل القيام المفقودة باستخدام الطرق الثلاث الأكثر شيوعا (الوسط الحسابي، نقطة الاتجاه الخطي، التقريب الخطي) باستخدام برمجيه (SPSS).

خامسا: إجراء التحليل العاملي التوكيدي للمجموعات المتعددة (MGCFA: Multiple Group Confirmatory Factor Analysis) للتحقق من أنواع التطابق في البناء العاملي للمقياس على البيانات الأصلية بمقابل البناء العاملي للمقياس على البيانات المعالجة بكل من الطرق الثلاث.

نتائج الدراسة وتفسيرها:

للإجابة عن سؤال الدراسة الذي ينص على:

“هل يختلف البناء العاملي لمقياس جودة الحياة باختلاف طريقة تعويض القيم المفقودة (الوسط الحسابي، نقطة الاتجاه الخطي، التقريب الخطي)؟”

للتأكد من صحة البنية العاملية للمقياس تم إجراء تحليل عاملي توكيدي باستخدام برمجية (AMOS) للنموذج المبين في الشكل (1).

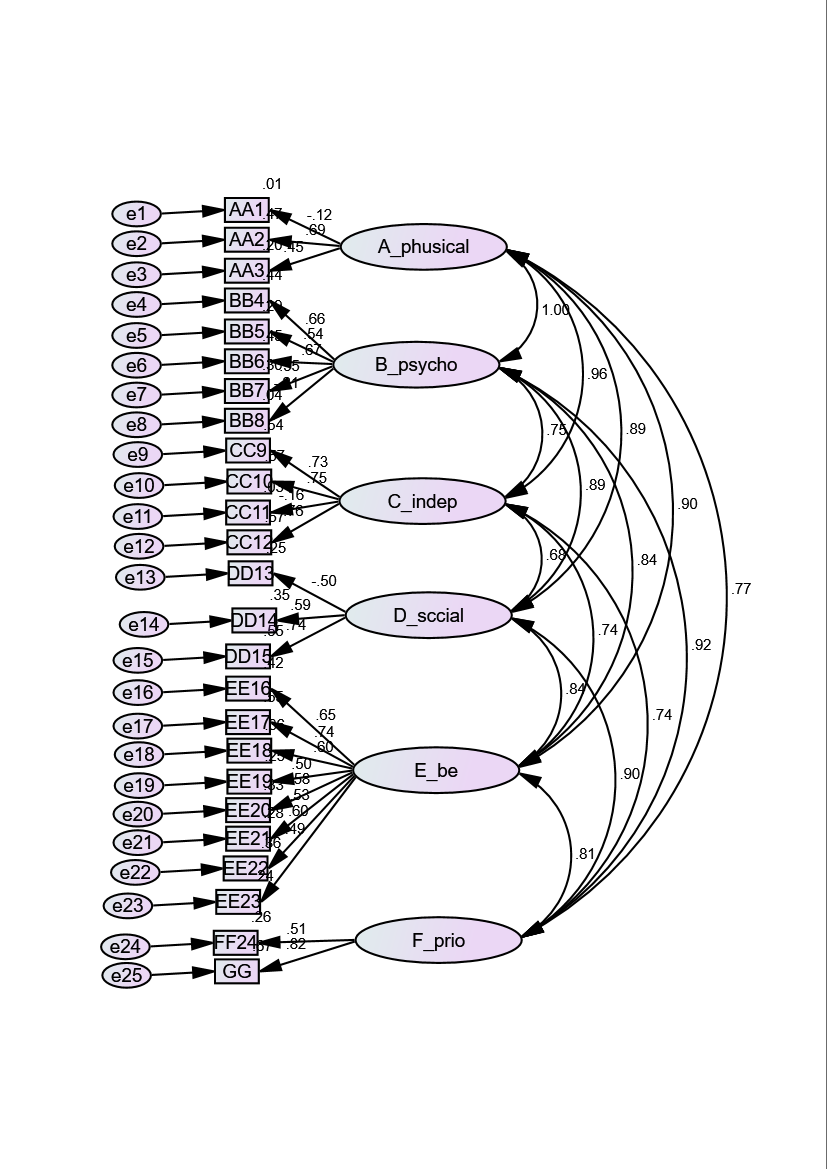
الشكل (1): النموذج العاملي المقترح “نظريًا” لمقياس جودة الحياة قبل التعديل

وبعد إجراء التحليل العاملي التوكيدي للمقياس على البيانات الأصلية تبين عدم مطابقة النموذج للبيانات بصورته الحالية وهذا ما يتضح من اغلب مؤشرات المطابقة المبينة في الجدول (1).

الجدول (1): مؤشرات المطابقة للنموذج المقترح.
مؤشر المطابقة	المعيار المعتمد	القيمة المستخرجة
df))	——–	260
2) )	——–	658.695
(P-value)	0.05 ≤	0.000
2/ df))	لا يتعدى (3.00)	2.533
CFI))	الحد الأدنى 0.80	0.801
TLI))	الحد الأدنى 0.80	0.770
(RMSEA)	الحد الأعلى 0.08	0.083

يلاحظ من الجدول (1) أن نسبة مربع كاي إلى درجات الحرية لم تتجاوز القيمة (3)، إلا أن فان قيم كل من (CFI، TLI) لم تتجاوز الحد الأدنى البالغ (0.8)، وكذلك فان قيمة (RMSEA) تجاوزت الحد الأدنى المقبول البالغ (0.08)، وهذا ما يؤكد عدم مطابقة النموذج للبيانات بصورته الحالية ولذلك تم إجراء تعديلات (Modification) للنموذج لتحسين جودة المطابقة تطلبت حذف فقرات لأحد العوامل الكامنة للخروج بنموذج مطابق كما هو مبين في الشكل (2).

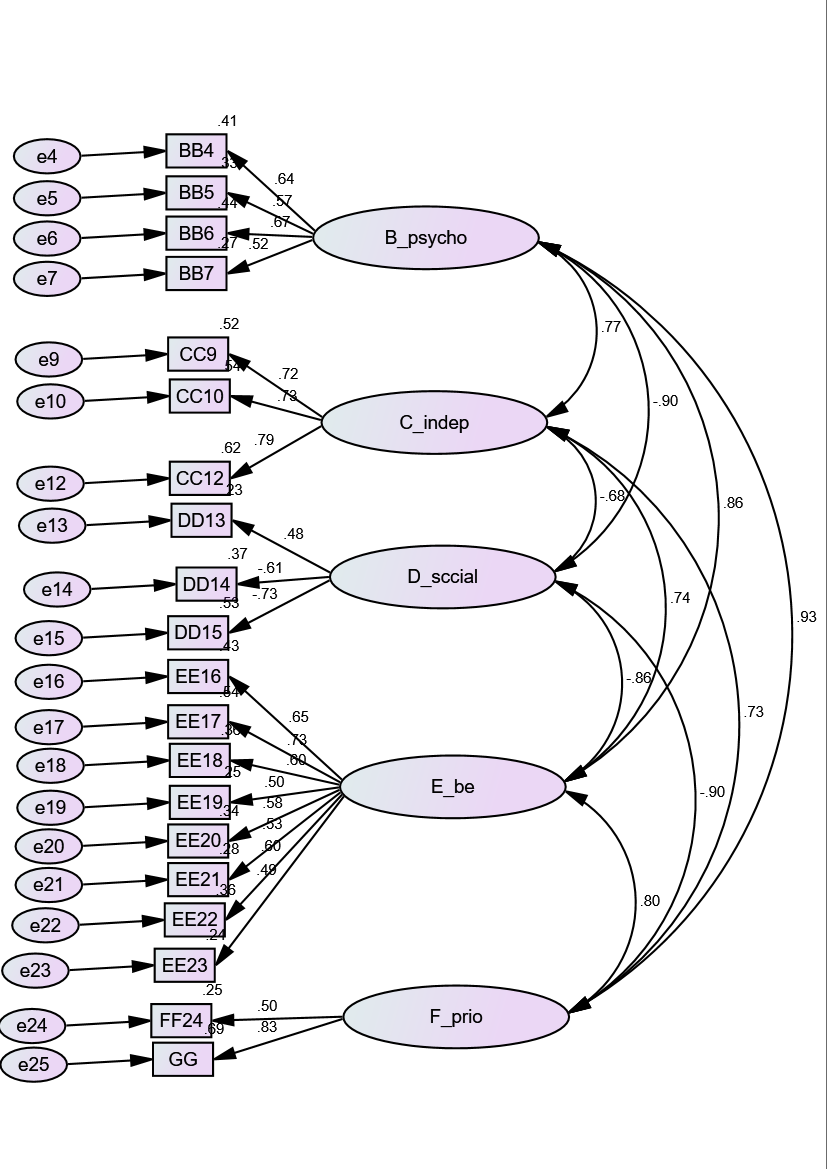
الشكل (2): النموذج العاملي المقترح لمقياس جودة الحياة بعد التعديل.

يتضح من الشكل (2) أن قيم تشبع كل من الفقرات على أبعادها أصبحت ضمن المستوى المقبول، وتبين مؤشرات المطابقة المبينة في الجدول (2) مطابقة البيانات للنموذج بالصورة المعدلة.

الجدول (2): مؤشرات المطابقة للنموذج المعدل.
مؤشر المطابقة	المعيار المعتمد	القيمة المستخرجة
df))	——–	160
2) )	——–	391.117
(P-value)	0.05 ≤	0.000
2/ df))	لا يتعدى (3.00)	2.444
CFI))	الحد الأدنى 0.80	0.859
TLI))	الحد الأدنى 0.80	0.833
(RMSEA)	الحد الأعلى 0.08	0.080

وللتحقق من مدى تطابق البناء العاملي باختلاف طريقة تعويض القيم المفقودة (missing values) تم استخدام التحليل العاملي التوكيدي للمجموعات المتعددة (MGCFA: Multiple Group Confirmatory Factor Analysis) وذلك في ضوء أربعة مستويات من التكافؤ (التكافؤ الشكلي (Configurable Invariance)، التكافؤ المتري (Metric Invariance)، التكافؤ القياسي (Scalar Invariance) والتكافؤ في البواقي (Residual Invariance)) على الترتيب، فاللاتغاير الشكلي أدنى مستوى من مستويات التطابق بين النماذج العاملية وأعلاها التكافؤ في البواقي، والجدول (3) يبين نتائج التحليل العاملي للمجموعات المتعددة للتحقق اللاتغاير في البناء العاملي عند تعويض القيم المفقودة بالطرق الثلاث:

أولا: طريقة الوسط الحسابي:

الجدول (3): مؤشرات المطابقة للنموذج المقترح المعدل للبيانات المعالجة بطريقة الوسط الحسابي.
مؤشر المطابقة	المعيار المعتمد	التطابق الشكلي	التطابق المتري	التطابق القياسي	تطابق البواقي
df))	——–	320	340	350	370
2) )	——–	750.781	755.105	755.773	758.833
(P-value)	0.05 ≤	0.000	0.000	0.000	0.000
2/ df))	لا يتعدى (3.00)	2.346	2.221	2.159	2.051
CFI))	الحد الأدنى 0.80	0.859	0.864	0.867	0.873
TLI))	الحد الأدنى 0.80	0.832	0.848	0.856	0.869
(RMSEA)	الحد الأعلى 0.08	0.055	0.052	0.051	0.048

يلاحظ من نتائج التحليل العاملي التوكيدي تحقق جميع أنواع التكافؤ (الشكلي، المتري، القياسي، البواقي) بين النموذج الأصلي والنموذج المعالجة القيم المفقودة في بياناته بطريقة الوسط الحسابي، حيث أن مؤشرات المطابقة في الحدود المقبولة بالنسبة لشكل النموذج، الأوزان الإنحدارية للفقرات على العوامل الكامنة باختلاف طريقة التدريج، وكذلك الأمر بالنسبة لمعاملات الارتباط بين العوامل الكامنة والبواقي.

ثانيا: طريقة نقطة الاتجاه الخطية:

الجدول (4): مؤشرات المطابقة للنموذج المقترح المعدل للبيانات المعالجة بطريقة نقطة الاتجاه الخطية.
مؤشر المطابقة	المعيار المعتمد	التطابق الشكلي	التطابق المتري	التطابق القياسي	تطابق البواقي
df))	——–	320	340	350	370
2) )	——–	751.014	755.347	756.024	759.135
(P-value)	0.05 ≤	0.000	0.000	0.000	0.000
2/ df))	لا يتعدى (3.00)	2.347	2.222	2.16	2.052
CFI))	الحد الأدنى 0.80	0.859	0.864	0.867	0.873
TLI))	الحد الأدنى 0.80	0.832	0.848	0.856	0.869
(RMSEA)	الحد الأعلى 0.08	0.055	0.052	0.051	0.048

يلاحظ من نتائج التحليل العاملي التوكيدي تحقق جميع أنواع التكافؤ (الشكلي، المتري، القياسي، البواقي) بين النموذج الأصلي والنموذج المعالجة القيم المفقودة في بياناته بطريقة نقطة الاتجاه الخطية، حيث أن مؤشرات المطابقة في الحدود المقبولة بالنسبة لشكل النموذج، الأوزان الإنحدارية للفقرات على العوامل الكامنة باختلاف طريقة التدريج، وكذلك الأمر بالنسبة لمعاملات الارتباط بين العوامل الكامنة والبواقي.

ثانيا: طريقة القيم التقريبية:

الجدول (5): مؤشرات المطابقة للنموذج المقترح المعدل للبيانات المعالجة بطريقة القيم التقريبية.
مؤشر المطابقة	المعيار المعتمد	التطابق الشكلي	التطابق المتري	التطابق القياسي	تطابق البواقي
df))	——–	320	340	350	370
2) )	——–	733.149	738.114	739.221	743.736
(P-value)	0.05 ≤	0.000	0.000	0.000	0.000
2/ df))	لا يتعدى (3.00)	2.291	2.171	2.112	2.01
CFI))	الحد الأدنى 0.80	0.862	0.867	0.87	0.875
TLI))	الحد الأدنى 0.80	0.836	0.852	0.859	0.872
(RMSEA)	الحد الأعلى 0.08	0.054	0.051	0.05	0.047

يلاحظ من نتائج التحليل العاملي التوكيدي تحقق جميع أنواع التكافؤ (الشكلي، المتري، القياسي، البواقي) بين النموذج الأصلي والنموذج المعالجة القيم المفقودة في بياناته بطريقة القيم التقريبية، حيث أن مؤشرات المطابقة في الحدود المقبولة بالنسبة لشكل النموذج، الأوزان الإنحدارية للفقرات على العوامل الكامنة باختلاف طريقة التدريج، وكذلك الأمر بالنسبة لمعاملات الارتباط بين العوامل الكامنة والبواقي.

يلاحظ من النتائج السابقة أن الطرق الثلاث المستخدمة لتعويض القيم المفقودة في مصفوفة البيانات تحافظ على البناء العاملي للمقياس ولا تختلف فيما بينها، ويمكن تفسير هذه النتيجة من خلال آلية عمل الطرق الثلاث في تعويض القيم المفقودة حيث أنها تعتمد على إحصائيات لتقدير القيم المفقودة وهي تسعى للوصول إلى نتائج لا تتأثر بالنقص في مصفوفة البيانات وهذا يعزز مفهوم صدق المقياس. حيث أن طريقة الوسط الحسابي تعوض القيمة التي تعتبر مقدر إحصائي لقيم المتغير، كذلك فان طريقة الانحدار تقدر قيم بناء على معادلة انحداريه تتأثر بمعامل انحداري وهو ما يمثل الوزن الإنحداري (Regression Wight) في البناء العاملي التوكيدي، وطريقة نقطة الاتجاه كذلك الأمر.

التوصيات:

في ضوء النتائج التي تم التوصل لها فان الباحث يوصي بما يلي:

• الاعتماد على طرق التعويض الثلاث (الوسط الحسابي، نقطة الاتجاه الخطي، التقريب الخطي) لعلاج القيم المفقودة بدلا من حذف الحالات.
• إجراء دراسة للتحقق صدق البناء للمقياس عند استخدام طرق الحذف.
• إجراء دراسة للتحقق من صدق البناء العاملي للمقياس عند استخدام طرق التعويض الأخرى.

المراجع

المراجع العربية:

العناتي، جهاد، اللبدي، نزار والمقصقص، محمد. (2018). مقارنة بين ثلاث طرائق للتعويض عن القيم المفقودة في الاختبارات العامة. دراسات-العلوم التروية، 45(1)، 1-17.

الصرايرة، راجي عوض (2018). أثر نسبة القيم المفقودة وطريقة معالجتها في دقة تقدير القيمة القصوى لدالة معلوماتية الفقرة وقيمة مؤشر ثبات الفقر. دراسات-العلوم التربوية، 45(4)، 485-501.

المراجع الأجنبية:

Allison, P. D. (2002). Missing data. Thousand Oaks, CA: Sage

Royston, P. (2005). Multiple imputation of missing values: Update. Stata Journal, 5, 88–102.

Cokluk, O., & Kayri, M. (2011). The Effects of Methods of Imputation for Missing Values on the Validity and Reliability of Scales. Educational Sciences: Theory and Practice, 11(1), 303-309.

Wickel, E. E. (2014). Reporting the reliability of accelerometer data with and without missing values. PloS one, 9(12), 221-207..

Weaver, B., & Maxwell, H. (2014). Exploratory factor analysis and reliability analysis with missing data: A simple method for SPSS users. The Quantitative Methods for Psychology, 10(2), 143-152.