د. علاء محمد علي البنوي1 هيثم محمد علي ناجي زريقات2
1 باحث في القياس والتقويم التربوي، وزارة التربية والتعليم الأردنية، هاتف رقم: 00962796337996؛ إيميل: albanawialaa@gmail.com.
2 باحث في القياس والتقويم التربوي، وزارة التربية والتعليم الأردنية، هاتف رقم: 00962788124449؛ إيميل: haiytham.zreqat@gmail.com.
HNSJ, 2022, 3(2); https://doi.org/10.53796/hnsj3230
تاريخ النشر: 01/02/2022م تاريخ القبول: 25/01/2022م
المستخلص
هدفت الدراسة الحالية التعرف على أثر نسبة القيم المفقودة على دقة التقدير وفق نموذج راش في ضوء طريقتي التقدير بييز والأرجحية العظمى، ولتحقيق ذلك اتبع الباحثان المنهج التجريبي حيث تم استخدام بيانات افتراضية تحاكي الظروف التجريبية المتمثلة في نسبة القيم المفقودة ولها مستويين (10%، 20%) وطريقة التقدير ولها مستويين (بييز، الأرجحية العظمى)، على عينة مكونة من (1000) مفحوص افتراضي واختبار مكون من (50) فقرة تم توليدها من خلال برنامج (wingen)، وقد توصلت الدراسة إلى أن الفروق في دقة التقدير تعزى لنسبة القيم المفقودة ولا تعزى لطريقة التقدير. ويتبين ان دقة تقدير الصعوبة أعلى عندما تكون نسبة القيم المفقودة (10%) منه عندما تكون نسبة القيم المفقودة (20%) حيث ان خطأ التقدير أعلى عندما تكون نسبة البيانات المفقودة أعلى. كما أن الفروق في دقة تقدير قدرة الأفراد تعود لطريقة بييز ولكل من النسبتين حيث أن خطا التقدير عند استخدام طريقة الأرجحية كان أعلى على الدوام. مع الانتباه لأن الفروق بين الطريقتين كانت أعلى عند نسبة الفقد (20%)، وقد أوصت الدراسة بالاعتماد على طريقة بييز في تقدير قدرة الأفراد عند وجود قيم مفقودة.
الكلمات المفتاحية: القيم المفقودة، دقة التقدير، بييز، الأرجحية العظمى، القدرة، الصعوبة.
The Impact of Missing Data Proportion on the accuracy of the estimate according to the Rasch model in light of the two methods of Bayesian estimation and the maximum likelihood
Dr. Alaa Muhammad Ali Al Banawi 1 Haitham Muhammad Ali Naji Zureikat2
1 Researcher in Educational Measurement and Evaluation, Jordanian Ministry of Education, Tel: 00962796337996; Email: albanawialaa@gmail.com.
2 Researcher in Educational Measurement and Evaluation, Jordanian Ministry of Education, Tel: 00962788124449; Email: haiytham.zreqat@gmail.com.
HNSJ, 2022, 3(2); https://doi.org/10.53796/hnsj3230
Published at 01/02/2022 Accepted at 25/01/2021
Abstract
The current study aimed to identify The Impact of Missing Data Proportion on the accuracy of the estimate according to the Rasch model in light of the two methods of Bayesian estimation and the maximum likelihood. To achieve this, the researchers followed the experimental approach. Where hypothetical data were used that simulate the experimental conditions represented in the Proportion of missing values and it has two levels (10%, 20%). and the method of estimation and has two levels (Bayesian, maximum likelihood). on a sample of (1000) hypothetical examinees. and component test Of (50) items generated through the (WinGen) program. the study concluded that the differences in the accuracy of the estimation are due to of Missing Data Proportion and not to the method of estimation. It turns out that the accuracy of estimating the difficulty is higher when the percentage of missing values is (10%) than when the percentage of missing values is (20%), as the estimation error is higher when the percentage of missing data is higher. In addition, the differences in the accuracy of estimating the ability of individuals are due to the Bayesian method and to each of the two ratios, as the error of estimate when using the odds method was always higher. Note that the differences between the two methods were higher at the percentage of loss (20%), and the study recommended relying on the Bayesian method in estimating the ability of individuals when there are missing values.
Key Words: missing values, estimation accuracy, Bayesian, maximum likelihood, ability, difficulty
المقدمة:
تختلف طرق التعامل مع القيم المفقودة الأمر الذي قد يؤدي إلى تقديرات ذات كفاءة أقل، فمنها ما يعتمد على الحذف ومنها ما يعتمد على إجراءات القيمية التعويضية، وفي ضوء وجود العديد من طرق التقدير وفقًا لنماذج نظرية استجابة الفقرة (item response theory)، فقد برز لدينا العديد من القضايا البحثية المتعلقة بدقة تقدير معالم الفقرات ومعلمة القدرة.
ومن الجدير بالذكر أن العالم يتز (Yates) كان اول من اتبع أسلوب الحذف للحالات التي تتضمن قيمًا مفقودة والاكتفاء بحجم العينة المتبقي بعد الحذف، ومن ثم ظهر أسلوب معالجة القيم المفقودة بالاعتماد التحليلات الإحصائية المتعلقة بالتباين والتباين المشترك على يد العالم بارتليت (Bartleet) في عام (1939) (الحيالي، 2013).
وقد توالت بعد ذلك الجهود في اقتراح أساليب متنوعة لمعالجة مشكلة البيانات المفقودة، باختلاف آلية الفقد سواء اكان فقدًا عشوائيًا تامًا تكون فيه القيم المفقودة مستقلة عن باقي القيم الأخرى، أم فقدًا عشوائيًا تكون فيه القيم المفقودة ذات علاقة بغيرها من قيم المتغيرات الأخرى وغير مرتبطة بالقيمة المفقودة نفسها، وأخيرًا الفقد الغير عشوائي والذي ينتج عن القيمة المفقودة نفسها وغير مرتبط بغيرها من القيم الأخرى (Little & Rubin, 1987).
وبما أن البحث الحالي يتعلق بفحص أثر نسبة القيم المفقودة على دقة التقدير وفق نموذج راش في ضوء طريقتي التقدير بييز والأرجحية العظمى، كان لا بد من التطرق إلى المفاهيم الأساسية في نموذج راش أحادي المعلمة، كأحد نماذج نظرية استجابة الفقرة (item response theory)، والتي جاءت كحل لتلافي أوجه القصور في النظرية الكلاسيكية (Classical Test Theory)، وبالأخص ما يتعلق بتأثر الخصائص السيكومترية للفقرات خصائص قدرات الأفراد المفحوصين، وكذلك تأثر درجات الأفراد المفحوصين بالخصائص السيكومترية للفقرات، وكذلك قصورها في معالجة تحيز الفقرات (Item bias) ومعادلة درجات الاختبار (Equating Test Scores) وبنوك الأسئلة (Embretson, & Reise, 2000).
ومن الافتراضات الأساسية للنظرية الحديثة (IRT) افتراض أن هناك قدرة واحدة فقط مسؤولة عن كيفية استجابة الافراد على فقرات الاختبار تسمى أحادية البعد (Unidimesionality)، وكذلك تستند نظرية الاستجابة للفقرة لافتراض آخر يتعلق بالعلاقة بين الفقرات المكونة للاختبار هو الاستقلال الموضعي (Local Independence)، وافتراض منحى خصائص الفقرة (Item Characteristic Curve) الذي يعكس العلاقة الحقيقية بين متغير القدرة والمتغيرات الملاحظة (الاستجابة على الفقرة ما) وتعرف بالعلاقة الوتيريه (Monotanicity) وافتراض يتعلق بخصائص الفقرات وعلاقتها بأداء المفحوصين (التحرر من السرعة) (speededness) (أبو علام، 2003).
ولقد بين هامبلتون (Hambleton & Swaminatham, 1985) ثلاث مزايا رئيسة لنظرية السمات الكامنة أو النظرية الحديثة في القياس هي:
أولاً: بافتراض وجود مجموعة كبيرة نسبياً من فقرات الاختبار التي تقيس نفس السمة، يكون تقدير قدرة الفرد مستقلاً عن عينة الفقرات التي تطبق عليه، أي إن تقدير قدرات الافراد متحررة من الفقرات (Item-free).
ثانياً: بافتراض وجود مجتمع كبير من الافراد تكون تقديرات الخصائص السيكومترية للفقرات (مثل معاملات الصعوبة والتمييز) مستقلة عن عينة الافراد التي استخدمت في تقدير هذه الخصائص اي لا تتأثر معالم الفقرات بالعينة المختارة من المجتمع (Person-free).
ثالثاً: يمكننا الحصول على احصائي مثل (الخطأ المعياري في التقدير) لتقدير درجة الدقة في قياس القدرة لكل فرد، وربما يختلف هذا الاحصائي من فرد الى اخر.
وفي هذا الصدد فقد أورد كل من هامبلتون وسومينثان وروجرز وكذلك أمبريتسون وريز (Hambelton, Swaminathan & Rogers, 1991) (Embretson & Reise, 2000) ثلاثة نماذج هي كما يلي:
1. النموذج اللوجستي أحداي المعلمة: يعرف هذا النموذج بنموذج راش وهو يفترض أن جميع فقرات الاختبار لا تختلف عن بعضها إلا بمعلمة الصعوبة (bi)، وهو بذلك يفترض تساوي معلمة التمييز (ai) لكافة الفقرات واقتراب معلمة التخمين (ci) من الصفر، إذ يتخذ هذا النموذج الصيغة الرياضية الآتية:
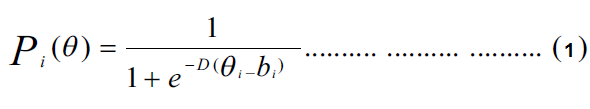
2. النموذج اللوجستي ثنائي المعلمة: يفترض هذا النموذج وجود اختلاف في كل من معلمتي الصعوبة والتمييز، مع بقاء احتمال اقتراب معلمة التخمين من الصفر كما هو في النموذج الأحادي، إذ يتخذ هذا النموذج الصيغة الرياضية الآتية:
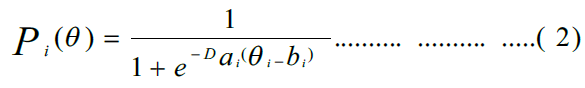
3. النموذج اللوجستي ثلاثي المعلمة: وهو النموذج الأكثر عمومية من باقي النماذج، إذ يضيف معلمة التخمين إلى النموذج الثنائي، ليتخذ هذا النموذج الصيغة الرياضية الآتية:
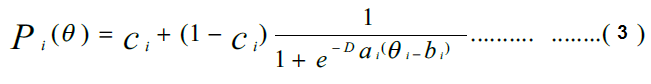
ومن الجدير بالذكر أن نظرية استجابة الفقرة قد قدمت مؤشرات إحصائية تشير إلى فاعلية الفقرة في تقديرها لمعلمة القدرة، ومثال ذلك ما يعرف بدالة معلوماتية الاختبار (Hambelton & Cook, 1977)، إذ تعرف المعلوماتية بأنها مؤشر الدقة لتقدير معلمة القدرة للفرد، إذ أن دقة التقدير تتطلب قدرًا كبيرًا من المعلوماتية حول القيمة العددية لمعلمة القدرة، والصيغة الرياضية لها تعطى من العلاقة الآتية:
……………………………………………..(4)
حيث تشير () إلى المعلوماتية، وتشير () إلى مربع الخطأ المعياري في التقدير، إذ ان قيمة دالة المعلوماتية تتراوح من (∞، -∞)، وكلما كانت قيمة دالة المعلوماتية كبيرة دل ذلك على دقة تقدير مرتفعة والعكس صحيح (Feriedrich, 2004).
كما أشار هامبلتون (Hambelton, 1989) الى أن دالة معلوماتية الفقرة عند مستويات القدرة المختلفة تعطى من خلال العلاقة الرياضية الآتية:

إذ تشير العلاقة الرياضية (5) إلى أن دالة معلوماتية الفقرة هي عبارة عن النسبة بين مربع المشتقة الأولى لاقتران منحنى خصائص الفقرة إلى تباين الأداء على الفقرة، وفي ظل أن الدراسة الحالية قد ركزت على نموذج راش فإن الصيغة الرياضية المستخدمة لحساب دالة معلوماتية الفقرة هي على النحو الآتي:
![]()
تقديرات المعالم في نظرية الاستجابة للفقرة:
1. طرق تقدير الأرجحية العظمى (Maximum Likelihood Estimation Methods):
يتم في هذه الطريقة تقدير المعالم من خلال إجراءات تعظيم الاحتمالية للمعلمة المراد تقديرها، عند توفر معلومات كافية عن عينة المفحوصين، إذ تعتمد هذه الطريقة على نمط استجابة المفحوصين على مجموعة من الفقرات تأخذ الإجابة الترميز (1، 0)، إلا أن أحد محددات هذه الطرقة تظهر عند إجابة المفحوص إجابة صحيحة أو خاطئة على كافة فقرات الاختبار، وبالتالي تصبح قدرته إما (-∞, ∞)، ومن محدداتها أيضًا عدم توفر القدرة في تقدير معالم الفقرات التي يجيب عليها جميع المفحوصين إجابة خاطئة أو صحيحة، لذا يتم حذف المفحوصين الذين يجيبون إجابات صحيحة أو خاطئة على جميع الفقرات، أو حذف الفقرات التي أجاب عليها كافة المفحوصين والتي لم يجب عليها أي مفحوص، للتغلب على هذه المحددات، كما يمكن أيضًا استخدام طريقة “بييز” بدلاً من عملية الحذف لتجنب هذه المحددات (Teresi, 2001).
2. طريقة تقدير بييز (Bayesian Estimation Method):
يتم اللجوء إلى هذه الطريقة لتلافي المحددات السابقة الذكر، والتي تمنع استخدام طرق الأرجحية العظمى، ومتماز باستخدامها لمعلومات أولية متوفرة من خبرات سابقة بالإضافة إلى استخدام معلومات عينة المفحوصين، وبهذا تساعد طريقة بييز في الحصول على تقديرات جيدة لمعالم الفقرات وقدرات المفحوصين، في حال توافرت معلومات عن توزيع القدرة لدى مجموعة من الأفراد المفحوصين (Garre & Vermunt, 2006).
مشكلة الدراسة:
تكمن مشكلة الدراسة الحالية في الكشف عن أثر نسبة القيم المفقودة على دقة التقدير وفق نموذج راش في ضوء طريقتي التقدير بييز والأرجحية العظمى، إذ تتحدد مشكلتها من خلال الفرضيتين الأتيتين:
H01: لا يوجد فروق ذات دلالة إحصائية عند مستوى الدلالة (α≤0.05) في تقدير معلمة الصعوبة تعزى لنسبة القيم المفقودة وطريقة التقدير.
H02: لا يوجد فروق ذات دلالة إحصائية عند مستوى الدلالة (α≤0.05) في تقدير قدرة الأفراد تعزى لنسبة القيم المفقودة وطريقة التقدير.
أهمية الدراسة:
تبرز أهمية الدراسة الحالية في محاولتها للكشف عن الفروق في تقديري معلمة القدرة للأفراد ومعلمة الصعوبة للفقرات، باختلاف نسبة القيم المفقودة وطريقة التقدير المستخدمة، وذلك للوصول على قرارا بشأن أي الطرق (بييز، الأرجحية العظمى) هي الأكثر نجاحا في تقدير كل من المعلمتين السابقتين في ضوء اختلاف نسب الفقد (10%، 20%).
أهداف الدراسة:
تهدف هذه الدراسة إلى تحديد أفضل الطرق في تقدير معلمتي الصعوبة وقدرة الأفراد في ضوء نسبتي الفقد (10%، 20%)، وذلك من خلال الآتي:
1. قياس الفروق في تقدير معلمة الصعوبة وفقًا لنسبة القيم المفقودة (10%، 20%) وطريقة التقدير (بييز والأرجحية العظمى).
2. قياس الفروق في تقدير معلمة القدرة للأفراد وفقًا لنسبة القيم المفقودة (10%، 20%) وطريقة التقدير (بييز والأرجحية العظمى).
مصطلحات الدراسة:
دقة التقدير: مؤشر إحصائي يعبر عن جودة تقدير المعلمة ويقاس بدلالة قيمة الخطأ المعياري للتقدير.
القيم المفقودة: ترك بعض المستجيبين لبعض الفقرات في الاختبار دون الإجابة عليها.
طرق التقدير: هو الأسلوب أو الطريقة الإحصائية المستخدمة في تقدير المعلمة (الصعوبة، القدرة).
محددات الدراسة:
1. اقتصرت الدراسة الحالية على استخدام كل من طريقتي بييز والأرجحية العظمى في تقدير معلمتي الصعوبة وقدرات الأفراد.
2. اقتصرت الدراسة الحلية على نسبتي الفقد في البيانات (10%، 20%).
3. تم توليد البيانات الخاصة بالدراسة من خلال برنامج (wingen) بواقع (50) فقرة و(1000) مستجيب وفقًا لنموذج راش أحادي المعلمة.
المنهج والإجراءات:
تم اتباع المنهج التجريبي حيث تم استخدام بيانات افتراضية تحاكي الظروف التجريبية المتمثلة في نسبة القيم المفقودة ولها مستويين (10%، 20%) وطريقة التقدير ولها مستويين (بييز، الأرجحية العظمى).
لتحقيق أهداف الدراسة تم اتباع الإجراءات التالية:
توليد عينة افتراضية من المستجيبين حجمها (1000) فرد تتبع قدرتهم التوزيع الطبيعي بمتوسط حسابي (0) وانحراف معياري (1)، باستخدام برمجية (WinGen).
توليد اختبار افتراضي تتبع فقراته نموذج راش أحادي المعلمة بمعلمة صعوبة تتبع التوزيع الطبيعي بمتوسط حسابي (0) وانحراف معياري (1)، باستخدام برمجية (WinGen).
توليد استجابات للأفراد في الخطوة (1) على الاختبار في الخطوة (2) لتتكون مصفوفة الاستجابات الافتراضية، باستخدام برمجية (WinGen).
إجراء فقد في مصفوفة الاستجابات بشكل عشوائي وبنسب مختلفة (10%، 20%) باستخدام برمجية اكسيل.
تعويض القيم المفقودة في كل من الاختبارين بعد إجراء الفقد بطريقة المتوسطات الحسابية (mean) من خلال برمجية (SPSS).
التحقق من افتراضات نظرية الاستجابة للفقرة كالاتي:
أحادية البعد من خلال التحليل العاملي بالاعتماد على نسبة التباين المفسر كما هو مبين في الجدول (1).
| الجدول (1): التحقق من أحادية البعد في الاختبار عند الفقد بنسب (10% و20%) | ||||
| نسبة الفقد في الاختبار | العامل | الجذر الكامن | نسبة التباين المفسر | نسبة الجذر الأول إلى الثاني |
| 10% | الأول | 7.571 | 15% | 6.079 |
| الثاني | 1.245 | 2% | ||
| 20% | الأول | 7.053 | 14% | 5.477 |
| الثاني | 1.288 | 3% | ||
- الاستقلال الموضعي من خلال حساب الإحصائيات باستخدام برمجية (LDID) حيث كانت نسبة الأزواج المستقلة أعلى بكثير من نسبة الأزواج غير المستقلة.
- منحنى خصائص الفقرة حيث تم التحقق من ذلك من خلال رسم منحنى خصائص كل من فقرات الاختبار ولكل حالة ناتجة من تقاطع الظروف التجريبية المتمثلة في (نسبة الفقد وطريقة التقدير) باستخدام برمجية (Bilog-MG3) كما هو مبين في الشكل (1).
| الشكل (1): منحنى خصائص الفقرة | ||
| نسبة الفقد | الطريقة | منحنى خصائص الفقرات |
| 10% | بييز | |
| 10% | الأرجحية | |
| 20% | بييز | |
| 20% | الأرجحية | |
- التحرر من السرعة وهو افتراض لا يمكن فحصه في ضوء البيانات الافتراضية المولدة.
استخدام برمجية (Bilog-MG3) لتحليل البيانات لكل من مصفوفتي البيانات بعد تعويض القيم المفقودة لتقدير معلمة الصعوبة والقدرة بطريقتين مختلفتين (بييز، والأرجحية العظمى).
مقارنة دقة التقدير في كلا الطريقتين ولكل من نسب الفقد من خلال مؤشر الدقة المتمثل في الخطأ المعياري(SE).
النتائج ومناقشتها:
تم الإجابة عن فرضيات الدراسة كما يأتي:
الفرضية الأولى: “لا يوجد فروق ذات دلالة إحصائية عند مستوى الدلالة (α≤0.05) في تقدير معلمة الصعوبة تعزى لنسبة القيم المفقودة وطريقة التقدير.”
للإجابة عن السؤال تم استخراج المتوسطات الحسابية والانحرافات المعيارية لخطأ تقدير معلمة صعوبة فقرات الاختبار باختلاف نسبة القيم المفقودة في ضوء طريقة التقدير كما هو مبين في الجدول (2).
| الجدول (2): المتوسطات الحسابية لخطأ تقدير معلمة صعوبة فقرات الاختبار في باختلاف نسبة الفقد وطريقة التقدير | ||||||
| الطريقة | بييز | الارجحية | ||||
| النسبة | المتوسط الحسابي | الانحراف المعياري | العدد | المتوسط الحسابي | الانحراف المعياري | العدد |
| 10% | .08938 | .008720 | 50 | .08966 | .008831 | 50 |
| 20% | .10108 | .011246 | 50 | .10128 | .011404 | 50 |
يلاحظ وجود فروق في المتوسطات الحسابية لدقة التقدير باختلاف نسبة البيانات المفقودة وطريقة التقدير وللكشف عن دلالة تلك الفروق الملاحظة تم إجراء تحليل تباين ثنائي كما هو مبين في الجدول (3).
| الجدول (3): تحليل التباين في خطأ تقدير الصعوبة العائد لكل من النسبة والطريقة. | |||||
| مصدر التباين | مجموع المربعات | درجة الحرية | متوسط المربعات | قيمة F | الدلالة |
| النسبة | .007 | 1 | .007 | 66.232 | 0.00 |
| الطريقة | 2.880E-6 | 1 | 2.880E-6 | .028 | .867 |
| التفاعل | 8.000E-8 | 1 | 8.000E-8 | .001 | .978 |
| الخطأ | .020 | 196 | .000 | ||
| الكلي | .027 | 199 | |||
يتضح من نتائج تحليل التباين عدم وجود تفاعل بين الطريقة ونسبة القيم المفقودة مما يستدعي دراسة الأثر الرئيسي لكل من الطريقة ونسبة القيم المفقودة كما هو مبين في الجدول (4).
| الجدول (4): تحليل التباين في خطأ تقدير الصعوبة العائد لكل من النسبة والطريقة. | |||||
| مصدر التباين | مجموع المربعات | درجة الحرية | متوسط المربعات | قيمة F | الدلالة |
| النسبة | .007 | 1 | .007 | 66.898 | 0.00 |
| الخطأ | .020 | 198 | .000 | ||
| الكلي | .027 | 199 | |||
| الطريقة | .000 | 1 | .000 | .021 | .884 |
| الخطأ | .027 | 198 | .000 | ||
| الكلي | .027 | 199 | |||
يتضح من نتائج تحليل التباين في دقة التقدير العائد لكل من النسبة والطريقة حيث يتضح ان الفروق في دقة التقدير تعزى لنسبة القيم المفقودة ولا تعزى لطريقة التقدير. ويتبين ان دقة تقدير الصعوبة أعلى عندما تكون نسبة القيم المفقودة (10%) منه عندما تكون نسبة القيم المفقودة (20%) حيث ان خطأ التقدير أعلى عندما تكون نسبة البيانات المفقودة أعلى.
ويمكن تفسير ذلك من خلال ما تشكله البيانات المفقودة من نقص في القدرة على تقدير المعالم حيث أن البيانات المفقودة تشكل جزء من مصفوفة البيانات التي يتم الاعتماد عليه في عملية التقدير وان تعويض قيم مكانها ما هو إلا استراتيجية لملء هذه المناطق الفارغة في مصفوفة البيانات بقيم محايدة متمثلة في متوسط استجابات الأفراد على الفقرة أو وسيط القيم المجاورة أو غيرها من الطرق وهذا التعويض يساعد في استخدام المصفوفة بشكلها التام ولكنه لا يسهم في التقدير بنفس كفاءة القيم الأصلية.
ويمكن تفسير عدم وجود اختلاف بين الطريقتين من خلال الآلية التي تنهجها كلا الطريقتين في تقدير معالم الفقرة وهي طريقة متشابهة في المبدأ العام ومختلفة في بعض المدخلات المتعلقة في توزيع الأفراد والتي لا تختلف باختلاف القيم المفقودة وبخاصة في وجود توزيعات قبلية وبعدية.
وقد جاءت هذه النتيجة مختلفة مع نتائج دراسة الطراونة (2011) والتي خلصت إلى أفضلية طريقة بييز في تقدير معلمة الصعوبة، وكذلك نتائج دراسة ضعضع وطومان وطيفور (2020) ودراسة كيم (Kim, 2007) التي خلصت إلى أن طريقة الأرجحية ذات أفضلية في تقدير معلمة الصعوبة.
الفرضية الثانية: “لا يوجد فروق ذات دلالة إحصائية عند مستوى الدلالة (α≤0.05) في تقدير قدرة الأفراد تعزى لنسبة القيم المفقودة وطريقة التقدير.”
للإجابة عن السؤال تم استخراج المتوسطات الحسابية والانحرافات المعيارية لخطأ تقدير قدرة الأفراد باختلاف نسبة القيم المفقودة في ضوء طريقة التقدير كما هو مبين في الجدول (5).
| الجدول (5): المتوسطات الحسابية لخطأ تقدير قدرة الأفراد باختلاف نسبة الفقد وطريقة التقدير | ||||||
| الطريقة | بييز | الأرجحية | ||||
| النسبة | المتوسط الحسابي | الانحراف المعياري | العدد | المتوسط الحسابي | الانحراف المعياري | العدد |
| 10% | .36366 | .068976 | 1000 | .40370 | .055875 | 1000 |
| 20% | .40484 | .051585 | 1000 | .45678 | .062296 | 1000 |
يتبين من الجدول (5) وجود فروق في المتوسطات الحسابية لدقة التقدير باختلاف نسبة البيانات المفقودة وطريقة التقدير، وللكشف عن دلالة تلك الفروق الملاحظة تم إجراء تحليل تباين ثنائي كما هو مبين في الجدول (6).
| الجدول (6): تحليل التباين في خطأ تقدير القدرة العائد لكل من النسبة والطريقة. | |||||
| مصدر التباين | مجموع المربعات | درجة الحرية | متوسط المربعات | قيمة F | الدلالة |
| النسبة | 2.222 | 1 | 2.222 | 616.168 | 0.000 |
| الطريقة | 2.115 | 1 | 2.115 | 586.595 | 0.000 |
| التفاعل | .035 | 1 | .035 | 9.813 | .002 |
| الخطأ | 14.407 | 3996 | .004 | ||
| الكلي | 18.779 | 3999 | |||
من نتائج تحليل التباين يتضح وجود تفاعل بين الطريقة ونسبة القيم المفقودة كما هو مبين في الشكل (2).
| الشكل (2): التفاعل بين الطريقة والنسبة في التأثير على دقة تقدير القدرة |
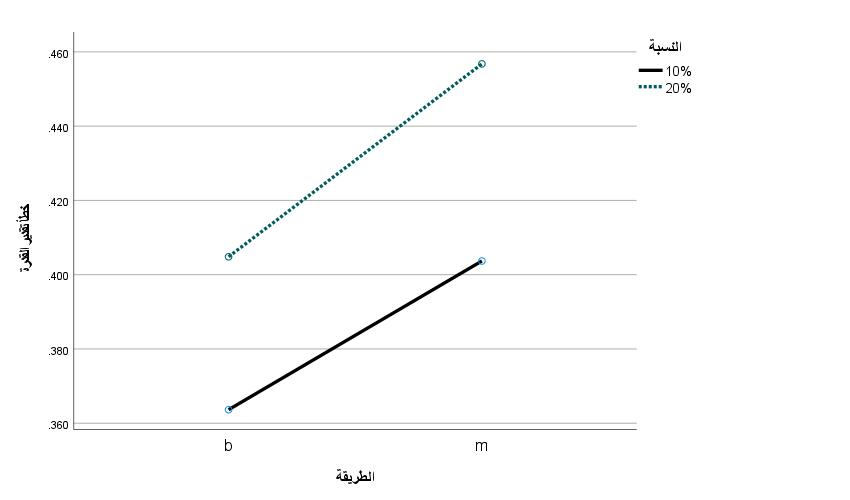 |
يتضح من الشكل وجود تفاعل بين النسبة والطريقة مما يستدعي دراسة التأثيرات البسيطة لكل من الطريقة ونسبة القيم المفقودة كما هو مبين في الجدول (6).
لذلك تم دراسة أثر الطريقة حسب نسبة الفقد حيث تم دراسة الفروق في دقة تقدير القدرة بين الطريقتين ولكل من نسبتي الفقد باستخدام تحليل التباين الأحادي كما هو مبين في الجدول (7).
| الجدول (7): تحليل التباين في خطأ تقدير الصعوبة العائد للطريقة لكل من نسبتي الفقد. | ||||||
| نسبة الفقد | مصدر التباين | مجموع المربعات | درجة الحرية | متوسط المربعات | قيمة F | الدلالة |
| 10% | الطريقة | .802 | 1 | .802 | 203.461 | 0.000 |
| الخطأ | 7.872 | 1998 | .004 | |||
| الكلي | 8.673 | 1999 | ||||
| 20% | الطريقة | 1.349 | 1 | 1.349 | 412.322 | 0.000 |
| الخطأ | 6.535 | 1998 | .003 | |||
| الكلي | 7.884 | 1999 | ||||
يتضح من نتائج تحليل التباين في دقة التقدير العائد للطريقة لكل من نسبتي الفقد ان الفروق دالة إحصائيا وهي لصالح طريقة بييز ولكل من النسبتين، حيث ان خطا التقدير عند استخدام طريقة الأرجحية كان أعلى على الدوام. مع الانتباه لان الفروق بين الطريقتين كانت أعلى عند نسبة الفقد (20%). وهو ما يمكن تفسيره من خلال التوزيعات القبلية المتعلقة بأفراد العينة والتي يفترض أن تتشابه مع التوزيعات في البيانات ومع وجود قيم مفقودة بنسب أعلى يصبح الفرق بين التوزيعات كبير، مما يظهر الطريقة بدقة تقدير أعلى حيث تقاس الدقة بالقدرة على إحداث الفروق بين التوزيعات.
وقد جاءت هذه النتيجة متفقة مع نتائج دراسة كل من ضعضع وطومان وطيفور (2020) ودراسة الرحيل والدرابسة (2014) والطراونة (2011) التي توصلت إلى افضلية طريقة بييز في تقدير معلمة القدرة للأفراد.
التوصيات:
في ضوء النتائج التي تم التوصل لها يوصي الباحثان بما يلي:
- الاعتماد على طريقة بييز في تقدير قدرة الأفراد عند وجود قيم مفقودة.
- إجراء دراسة للمقارنة بين طريقتي بييز والأرجحية في ضوء طريقة تعويض القيم المفقودة.
المصادر والمراجع:
أبو علام، رجاء محمود. (2003). التحليل الإحصائي للبيانات باستخدام برنامج (SPSS). ط1، القاهرة: دار النشر للجامعات.
الحيالي، علي درب كسار. (2013). استخدام معايير الدقة التنبؤية في تحديد الطريقة المثلى في تقدير القيمة المفقودة: بيانات البحوث الزراعية أنموذجًا. مجلة العلوم الزراعية العراقية، 44(4)، 509-517.
الرحيل، راتب صايل والدرابسة، رياض أحمد. (2014). أثر طريقتي التعامل مع القيم المفقودة، وطريقة تقدير القدرة على دقة تقدير معالم الفقرات والأفراد. المجلة الدولية التربوية المتخصصة، 3(6)، 23-47.
ضعضع، هبة وطومان، منار وطيفور، مصطفى. (2020). أثر حجم العينة وطرائق التقدير في دقة تقدير معالم نموذج راش. مجلة جامعة جرش، 21(1)، 131-170.
الطراونة، ارياف. (2011). المقارنة بين طرق تقدير القدرة باستخدام النموذج المناسب في ضوء الخطأ المعياري في تقديرها. رسالة ماجستير، جامعة مؤته.
Embretson, S.E., & Reise, S. P. (2000). Item Response Theory for Psychologists. New Jersey: Lawrence Erlbaum Associates, Publishers.
Embretson, S.E., and Reise, S. P. (2000). Item Response Theory for Psychologists. New Jersey: Lawrence Erlbaum Associates, Publishers.
Freidrich, S. (2004). A visual guide to item response theory. Ivailo Partchev.
Garre, F. & Vermunt, J. (2006). Avoiding boundary estimates in latent class analysis by Bayesian posterior mode estimation. Behaviormetrika, 33(1), 43-59.
Hambleton, R. & Swaminatham, H. (1985). Item Response theory: principles and application. Boston, MA: Kluwek NIJ puplishing.
Hambleton, R. K., Swaminathan, H., and Rogers, H. J. (1991). Fundamentals of Item Response Theory. London: Sage Publications, Inc.
Hambleton, R., and Swaminathan, H. (1985). Item Response Theory Principles and Applications. Boston Kluwer – Nijhoff Publishing.
Hambleton, R.K. (1989). Principles and Selected applications of Item Response Theory. InR. Linn (ed), Educational Measurement (3rd end). New York: Memillan. P: 147-200.
Hambleton, R.K., and Cook, L.L. (1977). Latent trait models and their use in the analysis of educational test data. Journal of Educational Measurement. 14(2). P: 75-94.
Kim, I. (2007). A Comparison of a Bayesian and Maximum Likelihood Algorithms for Estimation of a Multilevel IRT Model. PhD thesis, Athens, Georgia
Little, R., and Rubin, D. (1987). Statistical Analysis with Missing Data. New York. Wiely.
Teresi, A. (2001). Statistical Methods for Examination of Differential Item Functioning (DIF) with Applications to Cross-Cultural Measurement of Functional, Physical and Mental Health. Journal of Mental Health and Aging, 7(1):31-40.
