استخدام طريقة البوتستراب في التنبؤ بالقيمة المعرضة للخطر لعوائد سوق الأوراق المالية السعودية

فواز حسن احمد القاسمي1

1 أستاذ الإحصاء المساعد، كلية العلوم الإدارية، جامعة عدن، اليمن.

بريد الكتروني: fawazkassim20@gmail.com

HNSJ, 2023, 4(8); https://doi.org/10.53796/hnsj4816

تنزيل الملف

تاريخ النشر: 01/08/2023م تاريخ القبول: 21/07/2023م

المستخلص

هدفت الدراسة إلى وضع نموذج لتقلبات عوائد سوق الأوراق المالية السعودية (TASI) باستخدام المؤشر العام للأسهم TASI.SR اليومي للفترة من 19/01/2015 إلى 8/7/2023، تم تقدير تقلبات عوائد السوق باستخدام كل من نموذج EGARCH، ونموذج GJR-GARCH باستخدام التوزيع الطبيعي وتوزيع T، وتم استخدام طريقتين للتقدير هي طريقة الإمكان الأعظم وطريقة البوتستراب، وأظهر السوق توزيعًا غير طبيعيا لعوائد المؤشر، اذ يدل على تأثيرات ARCH وتجميع التقلبات في صورة عناقيد واستمرارها، في حين تم الكشف على وجود أثر للرافعة المالية اذ تؤدي إلى تقلبات عالية، ومن خلال الدراسة والتحليل تم التوصل الى ان نموذج GJR-GARCH بتوزيع (T) افضل من نموذج EGARCH بتوزيع (T)، كما ان طريقة البوتستراب اكثر دقة من طريقة الإمكان الأعظم في تقدير النماذج، كما توصلت الدراسة الى ان نموذج bootstrap-GJR-GARCH(1,1)-T، افضل النماذج الملائمة لاختبار التأثيرات غير المتماثلة لعوائد المؤشر العام في سوق الأوراق المالية السعودي.

الكلمات المفتاحية: نموذج EGARCH، GJR-GARCH، طريقة البوتستراب، المؤشر العام السعودي.

Research title

Using the bootstrap method to predict the value at risk of the returns of the Saudi stock market

Fawaz Hassan Ahmed Al Qasimi1

1 Assistant Professor of Statistics, College of Administrative Sciences, University of Aden, Yemen.

Email: fawazkassim20@gmail.com

HNSJ, 2023, 4(8); https://doi.org/10.53796/hnsj4816

Published at 01/08/2023 Accepted at 21/07/2023

Abstract

The study aimed to develop a model for the fluctuations of the stock market returns on the Saudi Stock Exchange (TASI) using the daily general stock index TASI.SR for the period from 19/01/2015 to 8/7/2023. The fluctuations of market returns were estimated using each of the EGARCH model , and the GJR-GARCH model using the normal distribution and the T distribution, and two estimation methods were used, the method of greatest possibility and the bootstrap method, and the market showed an abnormal distribution of index returns, as it indicates the effects of ARCH and the aggregation of fluctuations in the form of clusters and their continuity, while it was revealed that there is an effect of leverage Finance, as it leads to high fluctuations, and through the study and analysis it was concluded that the GJR-GARCH model with (Student) distribution is better than the EGARCH model with (student) distribution, and the bootstrap method is more accurate than the greatest possibility method in estimating models, and the study also concluded The bootstrap-GJR-GARCH(1,1)-T model is the best suited model for testing the asymmetric effects of the returns of the general index in the Saudi stock market.

Key Words: EGARCH Model, GJR-GARCH, Bootstrap Method, Saudi General Index.

المقدمة

توجد عدة طرق للتقدير تتصف بعضها بانها اكثر ملائمة مع طبيعة نوع ما من البيانات (بيانات منخفضة التكرار، بيانات متوسطة التكرار، بيانات عالية التكرار)، ولكن معظم تلك الطرق تتطلب افتراضات معينة حول المعالم او حول البيانات او حول التباين (حد الخطأ)، ولا نستطيع الوفاء بتلك الافتراضات وخاصة مع البيانات المالية عالية التكرار، لذا وجدت أساليب نمذجة متقدمة قادرة على التقاط تلك التأثيرات الامر الذي استدعى استخدام طرق متقدمة للتقدير، ومن هذه الطرق طريقة الامكان الاعظم (MLE) وطريقة البوتستراب bootstrap ، وطريقة شبه الإمكان الأعظم وطرق المحاكاة، وطريقة محاكاة العزوم وغيرها، ولكن تتطلب طريقة MLE افتراض التوزيع الطبيعي عند تقدير المعلمات والذي يصعب أحيانًا تحقيقه، وفي الوقت نفسه، لا تتطلب طريقة البوتستراب bootstrap افتراض التوزيع الطبيعي في تقدير المعلمات، فهي منهجية تقوم على إعادة أخذ عينات تهدف من خلالها إلى تحديد الخطأ المعياري المقدر لفترات الثقة لمعلمات المجتمع.

وفي البيانات المالية يعد التقلب مقياسًا للتغيير في العائد بمرور الزمن والتي تعد فيها نماذج التقلبات أحد أهم الخطوات في النمذجة المالية، حيث يمكن استخدام نموذج التقلب للتنبؤ بالحجم المطلق للعائدات أو كثافة التقلبات وتسعير الأصول واختيار المحفظة المالية، وتم استخدام عدد من النماذج في النمذجة المالية منها اسلوب الانحدار الذاتي المشروط بعدم تجانس حد الخطأ (ARCH) ونماذج الانحدار الذاتي الشرطية المعممة (GARCH)التي اصبحت من النماذج المهمة في دراسة وتحليل تقلبات بيانات السلاسل الزمنية المالية والتنبؤ بالقيمة المعرضة للخطر في الاسواق المالية، إذ يتطلب من المشاركين في السوق المالية اهتمام كبير بفترات التنبؤ بالعوائد المستقبلية كمقاييس لعدم التأكد وتوفير توقعات مكثفة لأسعار المحفظة المالية وتتبع جوانب معينة من هذه التوقعات مثل القيمة المعرضة للخطر.

ومع التأكيد بأن السلاسل الزمنية المالية تظهر عادةً أنماط عدم تناسق في التقلبات التي تسمى تأثيرات الرافعة المالية، تم إدخال عمليات GARCH غير المتماثلة للتحقيق في التقلبات غير المتماثلة، كما تم توجيه الكثير من الأبحاث إلى التقلبات غير الثابتة للتعامل مع فترات الصعود والهبوط المرتفعة المتكررة في السلاسل الزمنية المالية، وتتناول هذه الدراسة النماذج غير المتماثلة وغير الثابتة من نوع EGARCH، ونموذج GJR-GARCH وتقديرهما باستخدام كل من طريقة الإمكان الأعظم وطريقة البوتستراب، واستخدامها في دراسة ونمذجة التقلبات والتنبؤ بعوائد المؤشر العام السعودي، وبغرض تحقيق ما تسعى اليه الدراسة قسمت الى ثلاثة أجزاء الأول تناول الاطار العام للدراسة ويشمل منهجية الدراسة والدراسات السابقة، والثاني تناول الاطار النظري للدراسة، والثالث تناول الجانب التطبيقي، ثم النتائج والتوصيات.

الإطار العام للدراسة

وفي هذا الجزء تتناول الدراسة المنهجية والدراسات السابقة كما يلي:

اولا: منهجية الدراسة

  1. مشكلة الدراسة:

تتلخص مشكلة الدراسة في ايجاد نموذج قادر على التنبؤ بالقيمة المعرضة للخطر في السوق المالية السعودية، ونمذجة تلك التقلبات من خلال تقدير النماذج المقترحة باستخدام طريقة البوتستراب وطريقة الامكان الاعظم واجتياز النموذج كافة الاختبارات المختلفة (اختبارات المفاضلة، اختبارات التغطية)، وتتلخص مشكلة الدراسة بالإجابة على التساؤل التالي:

هل نماذج EGARCH، GJR-GARCH، غير المتماثلة قادرة على التنبؤ بالتقلبات المالية

لعوائد المؤشر العام لبورصة السعودية للأوراق المالية؟

وتتفرع منه التساؤلات الفرعية التالية:

  • ما مدى دقة التنبؤ بالقيمة المعرضة للخطر عند تقدير نماذج EGARCH، GJR-GARCH باستخدام طريقة الامكان الاعظم؟
  • ما مدى دقة التنبؤ بالقيمة المعرضة للخطر عند تقدير نماذج EGARCH، GJR-GARCH باستخدام طريقة البوتستراب؟
  • اي الطرق أفضل بالتنبؤ بالقيمة المعرضة للخطر في السوق المالية السعودية؟
  1. اهمية الدراسة:

تتمثل اهمية الدراسة في كونها تتناول طرق تقدير معلميه (الامكان الاعظم) ولا معلميه (البوتستراب) للتنبؤ بالقيمة المعرضة للخطر لعوائد المؤشر العام في سوق الاوراق المالية السعودية والمفاضلة بين الطريقتين وذلك من خلال استخدام نموذج EGARCH، ونموذج GJR-GARCH وتقديرهما باستخدام طريقة الإمكان الأعظم وطريقة البوتستراب ومدى قدرة الطريقتين بالتنبؤ بالقيمة المعرضة للخطر في سوق الاوراق المالية السعودية (المؤشر العام).

  1. اهداف الدراسة:

تهدف الدراسة الى:

  • تقدير نموذج EGARCH للقيمة المعرضة للخطر باستخدام طريقة الامكان الاعظم
  • تقدير نموذج EGARCH للقيمة المعرضة للخطر باستخدام طريقة البوتستراب.
  • تحديد النموذج الافضل والطريقة الاكثر دقة بالتقدير.
  • التنبؤ بالقيمة المعرضة للخطر في سوق الاوراق المالية السعودية.
  1. فرضيات الدراسة:

اعتمدت الدراسة على الفرضيات التالية:

الفرضية الاولى: لا تعطي طريقة البوتستراب تقديرا دقيقا لنموذج EGARCH، GJR-GARCH للمؤشر العام في سوق الأوراق المالية السعودية.

الفرضية الثانية: لا تعطي طريقة الامكان الاعظم تقديرا دقيقا لنموذج EGARCH، GJR-GARCH للمؤشر العام في سوق الأوراق المالية السعودية.

الفرضية الثالثة: لا يمكن التنبؤ بالقيمة المعرضة للخطر في سوق الاوراق المالية السعودية باستخدام طريقة البوتستراب.

  1. منهج الدراسة

لتحقيق اهداف الدراسة واختبار فرضياتها استخدمت الدراسة المنهج الوصفي والمنهج التحليلي، حيث استخدم المنهج الوصفي في عرض وتوصيف بيانات الدراسة، واستخدم المنهج التحليلي للتحليل والاستنباط والتنبؤ بالقيمة المعرضة للخطر، وقد اعتمدت الدراسة على لغة البرمجة الاحصائية R.

  1. حدود الدراسة

تتمثل حدود الدراسة بالفترة (19-1-2015م) الى (6-7-2023م) والمتمثلة بسلسلة زمنية يومية للمؤشر العام السعودي في سوق الاوراق المالية، وبعدد 1916 مشاهدة (بواقع خمس ايام في الاسبوع)

ثانيا: الدراسات السابقة

تناولت العديد من الدراسات القيمة المعرضة للخطر بصورتها العامة مستخدمة طرق تقدير مختلفة لتلك النماذج الا ان تلك الدراسات لم تستخدم طريقة البوتستراب وخاصة على المستوى العربي، وتناولت الدراسة الحالية بعض الدراسات كالتالي:

  1. دراسة عمر ومحمد (2022م) بعنوان ” التنبؤ بالقيمة المعرضة للخطر باستخدام نماذج GARCH في ظل وجود مقاطع هيكلية دراسة حالة المؤشر العام لبورصة أبو ظبي “، وهدفت الدارسة إلى مقارنة دقة التنبؤ بالمخاطر باستخدام نماذج GARCH في ظل وجود مقاطع هيكلية باستخدامـ عوائد المؤشر العام لبورصة أبو ظبي خلال الفترة (2015-2021م)، وتوصلت الدراسة الى ان نتائج التنبؤ خارج العينة بالقيمة المعرضة للخطر (95% VaR)، أكدت على أفضلية نماذج MSGARCH على النماذج التقليدية في ظل وجود مقاطع هيكلية.
  2. دراسة (Nurhayati,, 2022) بعنوان “ Value At Risk Prediction For The GJR-GARCH Aggregation Model” وكانت بعنوان ” التنبؤ بالقيمة المعرضة للخطر باستخدام نموذج GJR-GARCH “، وهدفت هذه الدراسة إلى التنبؤ بالقيمة المعرضة للخطر باستخدام نموذج GJR-GARCH (1,1)، حيث يعد التقلب بانه مستوى المخاطر التي تواجهها بسبب تقلبات الأسعار، وكلما زاد التقلب، زادت المخاطر ونحتاج إلى مقياس لتلك المخاطر مثل القيمة المعرضة للخطر (VaR) ونمذجة التقلب للتغلب على هذه القيمة، وفي أغلب الأحيان نموذج التقلب المستخدم في القطاع المالي هو GARCH ومع ذلك، لا يزال هذا النموذج غير قادر على استيعاب الطبيعة غير المتماثلة للتقلبات، لذلك تم تطوير نموذج GJR-GARCH بالإضافة إلى ذلك، استخدمت هذه الدراسة أيضًا النموذج التجميعي مع اثنين من الأصول فيها، وتم استخدام طريقة الإمكان الأعظم في تقدير النموذج، وتوصلت الدراسة الى أن التنبؤ بالتقلب باستخدام نموذج تجميع GJR-GARCH(1,1) أكثر دقة من نموذج تجميع GACRH(1,1) لأنه يحتوي على قيمة VaR صحيحة قريبة من مستوى الثقة المحدد.
  3. دراسة (Misha, 2021) بعنوان” Comparison of the GARCH, EGARCH,GJR-GARCH and TGARCH model in times of crisis for the S&P500, NASDAQ and Dow-Jones ” واتت بعنوان ” مقارنة بين نماذج GARCH وEGARCH وGJR-GARCH وTGARCH في أوقات الأزمات لمؤشرات S & P500 وNASDAQ وDow-Jones” وتهدف هذه الدراسة الى البحث في الأداء النسبي للتنبؤ بالتقلبات لنماذج GARCH وEGARCH و GJR-GARCH و TGARCH القياسية في أوقات الأزمات، بالتطبيق على الأسعار اليومية لمؤشرات S & P500 و NASDAQ و Dow-Jones. وتتكون فترة الدراسة من البيانات اثناء الازمات المختلفة(ازمة COVID-19، الازمة المالية العالمية) وتم الحصول على البيانات من خلال الانترنت، وتمت التوقعات على فترة خمس سنوات وتم اختبارها مقابل بعضها البعض باستخدام مقياسين للتقييم واختبارات Diebold-Mariano tests، وبالنسبة لجميع النماذج الأربعة، يتم اختبار التنبؤات التي تفترض التوزيع الطبيعي وتوزيع t، مقابل بعضها البعض، وتوصلت الدراسة الى أن توزيع t هو الأفضل لكافة النماذج باستثناء مجموعة واحدة من البيانات، وتمت مقارنة التوقعات التي تفترض توزيع t عبر النماذج الأربعة، وأظهرت النتائج أن GJR-GARCH الذي يعد من النماذج غير المتماثلة يتفوق على النماذج الاخرى بشكل كبير في كافة مجموعات البيانات.
  4. دراسة Ardia David et al,. 2018)) بعنوان ” Forecasting risk with Markov-switching GARCH models: A large-scale performance study واتت بعنوان التنبؤ بالمخاطر باستخدام نماذج GARCH التي تعمل بنظام تحويل ماركوف (Markov-switching) وهدفت الى القيام بإجراء دراسة تجريبية واسعة النطاق من أجل مقارنة أداء التنبؤ بنماذج GARCH ونماذج (MSGARCH) بتحويل ماركوف من منظور إدارة المخاطر، وتوصلت الدراسة الى أن نماذج MSGARCH تقدم توقعات أكثر دقة للقيمة المعرضة للخطر ، والنقص المتوقع ، والتنبؤ بتوزيع الذيل الايسر لعوائد الأسهم اليومية والأسبوعية و 10 أيام، كما توصلت الدراسة إلى أن حساب عدم اليقين في المعلمات يحسن تنبؤات الذيل الايسر.

الجانب النظري

في هذا الجانب تم التأطير النظري للدراسة والمتمثلة بنماذج EGARCH، GJR-GARCH وطرق التقدير والقيمة المعرضة للخطر كما يلي:

أولا: نماذج GARCH

تعد نماذج السلاسل الزمنية الخطية غير قادرة على شرح عدد من السمات المهمة المشتركة لكثير من البيانات المالية، بما في ذلك توزيعات الذيول الثخينة (leptokurtosis)، والتقلبات التجميعية وتأثيرات الرافعة المالية (بشكل أساسي لأنها تفترض أن التباين الشرطي ثابت)، كما انه من المهم ملاحظة بعض الحقائق للأصول المالية (عالية التردد)، اذ تحدث بشكل متكرر أكثر من المتوقع في ظل الحالة الطبيعية (ذيول ثخينة) والعوائد السلبية الشديدة تحدث بشكل متكرر أكثر من الإيجابية (عدم التماثل السلبي) ؛ فإن الطريقة الأساسية لتمثيل هذا النوع من البيانات هي استخدم نماذج التقلبات المشروطة بعدم تجانس التباين حيث تعطي نتائج مهمة؛ لأنها تسمح للتباين الشرطي لسعر السهم او المؤشر بالاعتماد على التباين في الفترة السابقة، (Wu, 2018, p6).

وسنلقي الضوء على اهم نماذج GARCH المستخدمة في دراسة السلاسل الزمنية المالية شديدة التقلب (عالية التكرار) والمستخدمة في هذه الدراسة، كما يلي:

  1. نموذج EGARCH

في عام 1991 قدم نيلسون نموذج GARCH الأسي، حيث اشار إلى أن نموذج EGARCH يمكنه التغلب على ثلاث عيوب رئيسية لنماذج GARCH العادية وهي:( Askar, 2013, p7)

  • الارتباط السلبي بين العوائد الحالية والمستقبلية والذي لم يستطيع نموذج GARCH استيعابه.
  • نماذج GARCH تفرض قيود على المعلمات.
  • لا تأخذ نماذج GARCH في الاعتبار تأثيرات التباين غير المتماثل.

لذا قدم نيلسون نموذج EGARCH الذي يسمح بتوصيف التأثيرات غير المتماثلة والذي يصف العلاقة بين الاخطاء في الماضي ولوغاريتم التباين الشرطي بدون أي قيود تفرض على المعالم وتأكيد عدم سالبية التقلبات ، ويعطى النموذج الاسي بالصورة التالية: (Christian and Zakoıan: 2010:P246)

حيث ، وباستخدام خصائص ان الدالة يكون متوسطها الصفر وتكون غير مرتبطة، كما يمكن اعادة كتابتها بصورة خطية على النحو التالي:

حيث يكون تأثير الاخطاء السالبة على لوغاريتم التباين الشرطي هو وتأثير الاخطاء الموجبة على التباين الشرطي هو وهذه الخاصية تجعل النموذج يسمح بتوصيف او التقاط التأثيرات غير المتماثلة.

  1. نموذج GJR-GARCH

قدم Glosten et al(1993) نموذج العتبة للتقلبات الشرطية GJR-GARCHكأسلوب اخر لالتقاط التأثيرات غير المتماثلة للنبضات او التذبذبات الموجبة والسالبة على التقلب، حيث يرى Glosten ان حركة الهبوط في الغالب هي اعلى من حركة الصعود (التعافي)، مما يشير الى وجود تقلبات غير متماثلة وكبيرة وغير قابلة للقياس لكن يمكن نمذجتها من خلال نموذج GJR-GARCH . (Amiri et al, 2022, p172)

ويتم الحصول على النموذج من نموذج GARCH (1,1) وذلك بافتراض ان المعلمة تعتمد على اشارة التذبذب / النبضة، أي ان: (Christian and Zakoıan: 2010:P250)

حيث هي دالة اشارة النبضة / الصدمة وتعبر عن الرافعة المالية (الفعالية) وهي عبارة عن دالة يستخدم فيها المتغير الوهمي، وتكون شروط عدم سالبية التباين الشرطي هي

و وبالتالي فان التباين غير الشرطي هو:

ويعد نموذج GJR-GARCH نموذج مناضر للنموذج الاسي EGARCH ويعطي النموذجين نتائج متقاربة إذا استخدما لنفس السلسلة الزمنية.

ثانيا: القيمة المعرضة للخطر المعتمدة على نماذج GARCH

تعرف القيمة المعرضة للخطر على أنها أقصى خسارة محتملة في فترة زمنية معينة وعند مستوى ثقة معين في ظل ظروف السوق الاعتيادية. (Hidayana, 2022, p144)

وتعرف القيمة المعرضة للخطر على أنها الخسارة المتوقعة عند مستوى ثقة محدد خلال فترة زمنية معينة، وبرز مفهوم القيمة المعرضة للخطر كأبرز مقياس لمخاطر السوق السلبية من خلال وضع حدًا أدنى للخسائر عند مستوى ثقة معين ومن خلال توقع معين، وبناء على نموذج القيمة المعرضة للخطر، ستتجاوز الخسائر المحققة حد القيمة المعرضة للخطر باحتمال صغير قيمته 𝛼، يتم اختياره عادةً بين 1٪ و 5٪. (Naimian, 2021, p6)

وتعطى الصيغة العامة للقيمة المعرضة للخطر بالآتي: ( Askar, 2013, p13)

حيث: هي احتمال الخسارة التي تتجاوز أو تساوي القيمة المعرضة للخطر، الخسارة او الربح، دالة كثافة الاحتمال لــ

ويتم حساب القيمة المعرضة للخطر للعائدات المركبة باستمرار من خلال الاتي:

ثالثا: طرق التقدير

اعتمدت الدراسة على طريقتين في التقدير احداها معلمية وتتمثل بطريقة الامكان الاعظم (LM) والثانية لا معلمية وتتمثل بطريقة البوتستراب Bootstrap كما يلي:

1- طريقة الإمكان الأعظم

وهـي الطريـقة الاكثـر شيـوعـا، وهي ” طـريـقـة تـكـراريـة تـعـتـمـد على تـكـرار العمليات الحسابية عـدة مـرات حتى يتم الوصول الى أفضل تقـديرات للمعلمات ” وهي تعـد من اكـثر الطرق مـلائمة للـنـماذج الخطيـة وغيـر الخطيـة كـافـة. (Wu, 2018, p9).

وبالنسبة لنماذج التباين الشرطي، تكون عملية التقدير ، و تتبع التوزيع الطبيعي او توزيع T بدرجات حرية ، كما يتبع عملية التباين الشرطي لكل من نموذج EGARCH ونموذج GJR-GARCH او نماذج GARCH في المتوسط وفق الصورة الاتية: (Amiri et al, 2022, P176)

ويتم تقدير معلمات نماذج EGARCH وGJR-GARCH باستخدام طريقة الإمكان الاعظم من خلال تقدير متجه المعلمات، وبافتراض ان هي البيانات التاريخية لمتغير عشوائي يتبع توزيع متماثل خلال الزمن وله دالة كثافة احتمالية ولتقدير متجه المعالم لا بد من إيجاد دالة الإمكان كما يلي: (Nurhayati, 2022, p3)

ثم إيجاد لوغاريتم دالة الإمكان من خلال:

ويتم الحصول على تقدير المعلمات من خلال تفاضل دالة الإمكان لمتجه المعالم ومساواتها بالصفر ، فاذا أردنا تقدير احدى المعلمات من متجه المعالم نـقـوم بـاشـتـقـاق الـمـعـادلـة الـمـذكـورة آنـفـاً نـسـبـة للمعـلمـة المراد تقـديـرهـا ومن ثم نساويها بالصفر لنحصل على مجموعة من المعادلات التي يمكـن حـلها باستـخـدام خوارزمية تكرارية تعرف بخوارزمية المـربعات الصغرى التكرارية الموزونة.

2- طريقة البوتستراب

طـور العـالـم (Efron) عـام (1979) طـريقـة جـديدة لإعـادة المـعـاينـة بـالإرجـاع سمـيت بطـريـقـة البـوتـستـراب (Bootstrap) وهي اعـادة عينـة تشتمـل على (n) مـن العـنـاصـر المسحـوبـة بـالإرجـاع بشكـل عشوائي من (N) من البيانات الاصلية (and Resheed, 2010,p21 Algamal)

وهي احـدى طرق الاحصـاء الاستنتاجيـ التي تتضمـن تقـديـر معـلمات المجتمـع او حساب فتـرات الثقـة أو اختبار الفـرضيات او غيـرهـا، إذ أن الاحصـاء الاستنتاجي يستخدم للاستـدلال عــن معالم المجتمـع وقيـاس ثقـة هـذه الاستنتـاجـات من خلال استخدام معـلـومـات مكـتسبـة مـن العينة وتعميمها على المجتمع، وان طـريقـة البـوتستراب تـزودنـا بتـقـديـرات للخـطـأ المعيـاري والتـحيـز عـن طـريـق (N) مـن العينـات البـوتسترابيـة المـأخـوذة بـالإرجـاع مـن العينـة الاصـليـة. (Martinez and Martinez, 2011, p88)

كما ان الطريقة المستخدمة على نطاق واسع هي إجراء التقدير المكون من خطوتين الأولى يتم تقدير معلمات نموذج التقلب المشروط EGARCH ، GJR-GARCH باستخدام احدى طرق التقدير المناسبة ومنها طريقة الإمكان الأعظم (ML) ، وبناءً على البواقي للنموذج المقدر تتم عملية التقدير، وفي الخطوة الثانية بالنسبة لأحجام العينات الواقعية (على سبيل المثال 500 أو 1000 ملاحظة يومية) ، فإنه يتم حذف المشاهدات التي نتج عنها بواقي عالية، حيث تخضع تلك البواقي لمخاطر تقدير كبير، و على وجه الخصوص، فإن عدم اليقين في التقدير المرتبط بالمقدر الكمي كبير بالنسبة للقيم/ البواقي المتطرفة. (Heinemann, 2019, P94)

وتتم خطوات البوتستراب من خلال الاتي:

  • اخذ عينة ( )، واحتساب مقدر الإمكان (ML) للمعلمة من خلال:
  • التباين الشرطي من خلال الصيغة: و
  • تقدير البواقي من خلال و
  • احتساب البواقي المعيارية من الصيغة
  • سحب عينة البوتستراب من البواقي المعيارية
  • استخدام وعينة البوتستراب في احتساب عينة بواقي البوتستراب من خلال الاتي:

ومن خلال بواقي البوتستراب يمكن أيضًا إنشاء فترات ثقة للمعالم المقدرة والتنبؤ بالقيم المستقبلية للسلسلة الزمنية وللتقلبات.

رابعا: اختبارات التقييم

بعد استخدام طرق مختلفة في تقدير القيمة المعرضة للخطر، نحتاج إلى التحقق من دقة النماذج المقدرة وقدرتها على التنبؤ، ويتم ذلك من خلال استخدام اختبارات إحصائية مختلفة للمفاضلة بين النماذج، بالإضافة الى اختبارات اكياك (AIC) وشوارتز (BIC)، وهناك العديد من اختبارات التقييم للقيمة المعرضة للخطر، حيث تعتمد الدراسة ثلاثة مقاييس لدقة التقييم وهي: دالة الخسارة الثنائية (اختبار الخسارة)، اختبار التغطية غير المشروطة، واختبار نسبة الامكان (LR) للتغطية غير المشروطة. (Nurhayati, 2022, p3)

  1. اختبار الخسارة الثنائية (نسبة الخسارة)

إذا كانت القيمة المعرضة للخطر المتوقعة غير قادرة على تغطية الخسارة المحققة، فإن هذا يسمى خسارة، ويعد اختبار نسبة الخسارة (VR) انعكاس لاختبار التغطية غير المشروط (LR) ، وتعطي عقوبة جزاء واحدة لكل استثناء من القيمة المعرضة للخطر، ويمكن تعريف VR على النحو التالي: ( Askar, 2013, P18)

حيث:

عدد التجاوزات الفعلية المرصودة.

مستوى احتمال القيمة المعرضة للخطر وتساوي هنا 0.05، 0.01.

عدد المشاهدات المستخدمة في التنبؤ بالقيمة المعرضة للخطر.

ولكي يكون التقييم دقيق يجب ان تكون قيمة الاختبار ما بين (0.5، 1.5) اما إذا كانت قيم VR> 1.5 أو VR <0.5 تعد نسبة الخسارة كبيرة. ويعد هذا الاختبار سهل لكنه غير قادر على اظهار الأسباب الكامنة عن فشل النموذج.

  1. اختبار التغطية غير المشروطة

ويقوم اختبار التغطية غير المشروطة او اختبار Kupiec’s على تحديد مدى اتساق الخسائر عن مستوى الثقة المحدد، ويبنى الاختبار على ان حالات الخسارة تتبع توزيع ذو الحدين، ولإجراء الاختبار نحتاج إلى عدد حالات الخسارة الفعلية (E)، وعدد المشاهدات (N) ومستوى احتمالية القيمة المعرضة للخطر (p)، وبافتراض ان حالات الخسارة E تتبع توزيع ذو الحدين Bin(N,P) فإن الفرضية الصفرية هي: (Naimian, 2021, p15)

وتقدر قيمة p من خلال وتكون نسبة الإمكان للاختبار هي:

يتـم رفض النموذج عند قبول الفرض البديل وذلك عند تجاوز احصائية القيمة الحرجة .

  1. اختبار التغطية الشرطي

قدم Christoffersen عام 1998م اختبارًا يعتمد على التغطية المشروطة، والذي يسمى أيضا باختبار الاستقلالية، وكما هو مبين أعلاه، يعد اختبار Kupiec اختبارًا للتغطية غير المشروطة لأنه لا يأخذ في الاعتبار استقلالية الانتهاكات أو التجاوزات او الخسائر، وللتحقق من مجموعة التقلبات في نموذج المخاطر، يحدد هذا الاختبار فيما إذا كانت الانتهاك او الخسائر قد حدثت في يوم معين بشرط الاعتماد على الانتهاكات او الخسائر في اليوم السابق له، (Nurhayati, 2022, p5)

ويعطى اختبار التغطية المشروطة بالصيغة: (Naimian, 2021, p16)

حيث ان:

عدد التجاوزات الفعلية المرصودة.

مستوى احتمال القيمة المعرضة للخطر وتساوي هنا 0.05، 0.01.

عدد المشاهدات المستخدمة في التنبؤ بالقيمة المعرضة للخطر.

ويتم رفض الفرضية الصفرية إذا كانت نتيجة اختبار الاستقلالية أكبر من

الجانب التطبيقي

يتمثل الجانب التطبيقي بوصف البيانات واختبارات النماذج واختبار الاستقرارية وتقدير النماذج باستخدام طريقة الإمكان الأعظم وطريقة البوتستراب واختبارات التغطية للقيمة المعرضة للخطر، كما يلي:

أولا: التحليل الوصفي

تعتمد الدراسة في الجانب التطبيقي على بيانات أسعار الاغلاق اليومي لمؤشر السعودية العام لسوق الأوراق المالية السعودي (TASI) لأيام التداول خلال الفترة (19-1-2015م) وحتى تاريخ (6-7-2023م) بواقع 1916مشاهدة، أما عوائد مؤشر السعودية العام تم حسابها باستخدام التحويل اللوغاريتمي وفق الصيغة:

حيث ان:

تمثل سعر الاغلاق لمؤشر السعودية العام عند الزمن t.

تمثل سعر الاغلاق لمؤشر السعودية العام عند الزمن t-1.

عائد المؤشر عند الزمن t.

  1. التمثيل البياني للمؤشر العام TASI

تم ايجاد الرسم البياني للمؤشر العام لسوق الأوراق المالية السعودي (TASI.RS) الذي يتكون من (227) مؤشر، وذلك لمعرفة الصورة الاولية لاتجاهات أسعار الاسهم خلال فترة الدراسة، والشكل (1) يبين اتجاه المؤشر العام السعودي خلال الفترة (19-1-2015 الى 6-7-2023).

شكل (1)

السلسلة اليومية للمؤشر العام السعودي (TASI.RS)

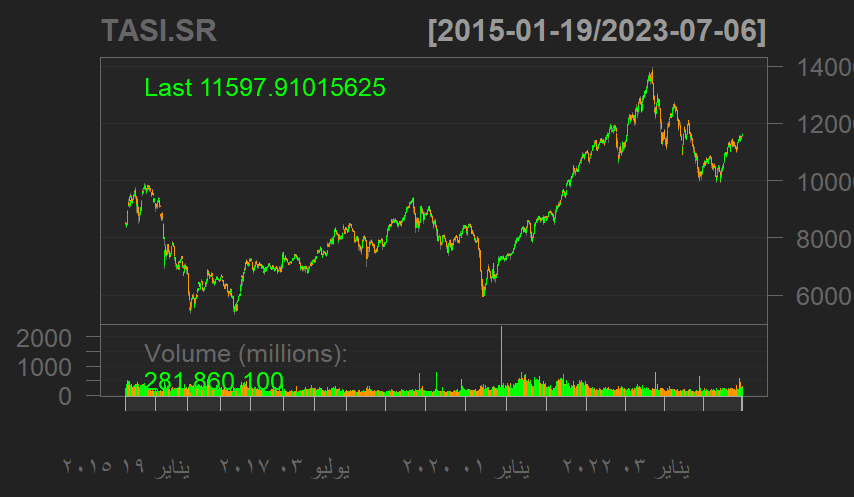
المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

ونلاحظ من خلال الشكل (1) التذبذب والتقلب السريع للمؤشر العام لأسعار الأسهم السعودي حيث اخذ اتجاها تصاعديا وتنازليا وكان أدني هبوط له خلال فترة الدراسة هو بداية العام 2016م ثم عاود بالارتفاع في الربع الأخير من نفس العام، وعاود بالانخفاض ثم ارتفع متدرجا ليصل الى اعلى ارتفاع له خلال فترة الدراسة في نهاية العام 2022م، كما تستخدم سلسلة المؤشر العام في حساب سلسلة العائد باستخدام طريقة حساب العائد

حيث تم حساب سلسلة العائد وتم تمثيلها بيانيا في الشكل (2)

شكل (2)

سلسلة العائد اليومي للمؤشر العام السعودي (TASI.RS.return)

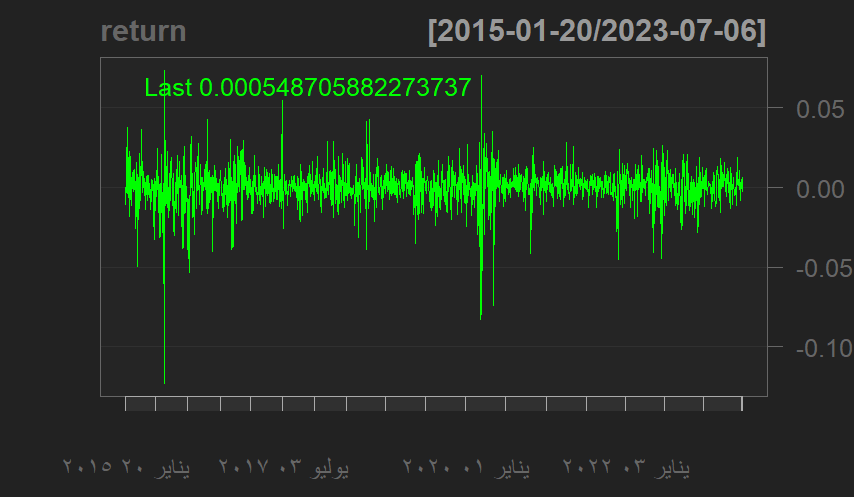
المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

  1. مقاييس الإحصاء الوصفي للمؤشر

تم استخراج مقاييس الإحصاء الوصفي لعائدات سعر الاغلاق للمؤشر العام السعودي خلال الفترة (19-1-2015 الى 6-7-2023)، وتم عرضها في الجدول (1)

جدول (1)

مقاييس الإحصاء الوصفي لعائدات المؤشر العام السعودي (سعر الاغلاق)

Mean Median Maximum Minimum sigma Skewness Kurtosis JB
-0.00007 -0.0003 0.03772 -0.0309 0.0000 0.9581 12.0525 0.000

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

ونلاحظ من خلال الجدول (1) ان متوسط العوائد قريب جدا من الصفر ويشير إلى ان هناك مجموعة واسعة من التقلبات، كما يشير معامل الالتواء الى ان العوائد غير متماثلة تماما ومنحنية قليلا نحو اليمين، بينما تشير القيمة الإيجابية للتفرطح إلى ان عوائد المؤشر العام تتبع توزيع الذيول الثخينة مما يشير الى ان غالبية العوائد تتجمع على ذيل التوزيع، والعديد من النقاط العنقودية بعيدًا عن المتوسط، ووفقًا لهذا التوزيع يجب الحذر للغاية بشأن القيمة المعرضة للخطر، والشكل (3) يعرض منحنى توزيع العوائد.

شكل (3)

توزيع سلسلة العائد مقارنة بالتوزيع الطبيعي (TASI.RS.return)

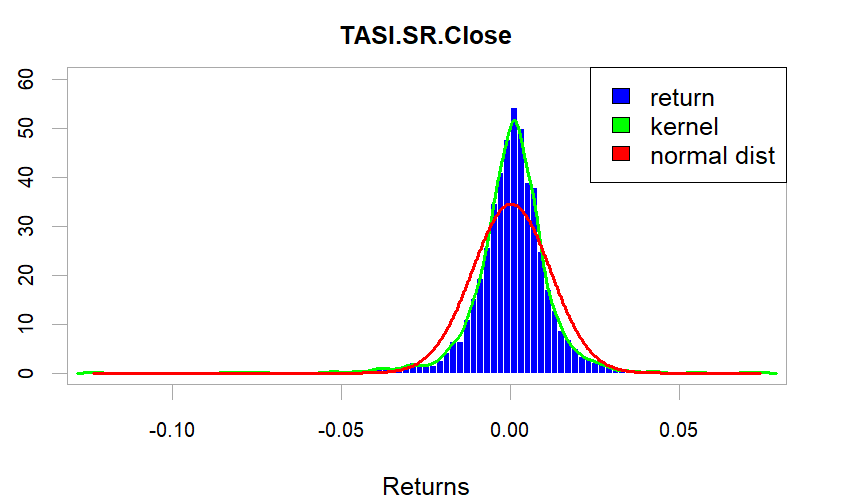
المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

  1. اختبار أثر ARCH

لكون السلسلة هي سلسلة العائد لذا فهي مستقرة تماما؛ الا انها في الغالب تعاني من ارتباط ذاتي، بالإضافة الى وجود أثر للتقلبات، لذا أجرى الباحث اختبار الارتباط الذاتي والارتباط الذاتي الجزئي لسلسة العائد وسلسلة مربع العائد للمؤشر العام السعودي، وكانت نتيجة اختبار الارتباط الذاتي كما في الشكل (4)، (5)، (6)

شكل (4) الارتباط الذاتي والارتباط الذاتي الجزئي لسلسلة العائد اليومي للمؤشر العام السعودي

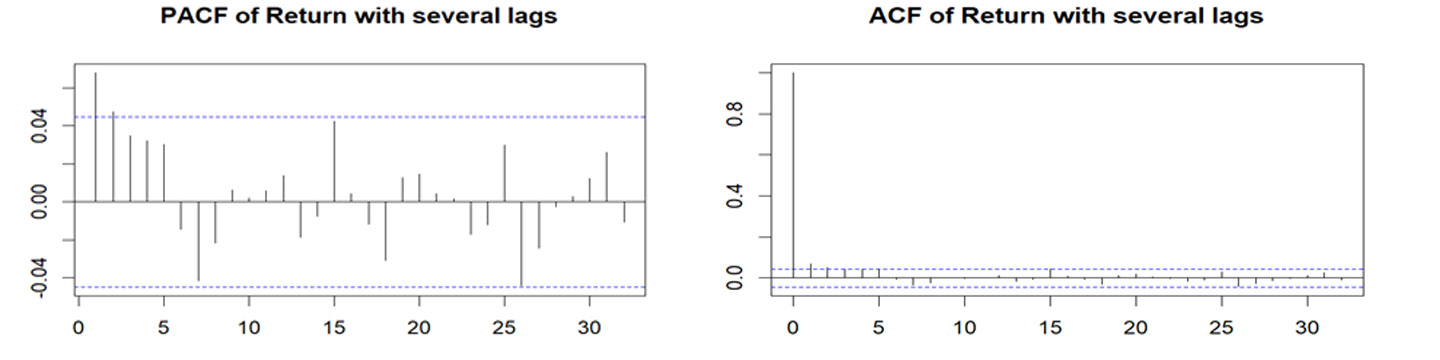
شكل (5) الارتباط الذاتي والارتباط الذاتي الجزئي لمربع سلسلة العائد اليومي للمؤشر العام السعودي

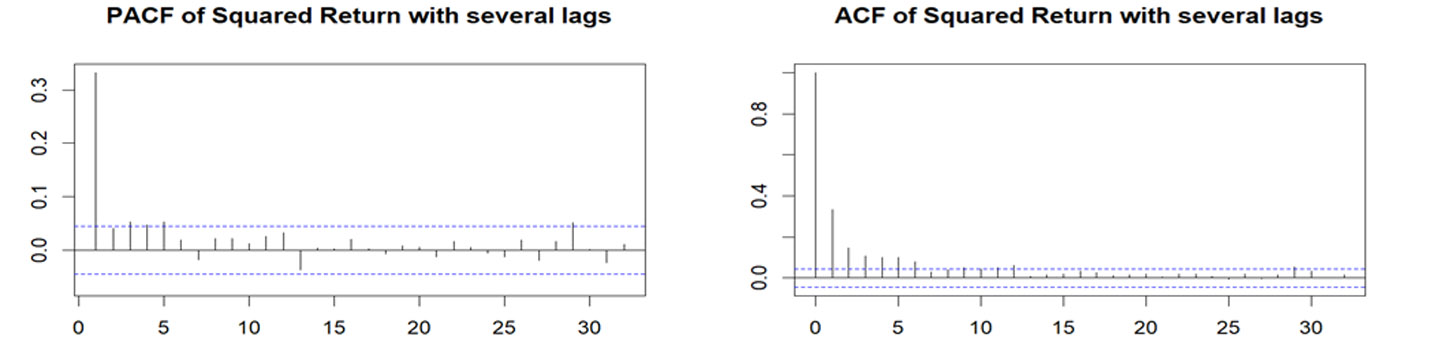
شكل (6) سلسلة العائد ومربع العائد اليومي للمؤشر العام السعودي

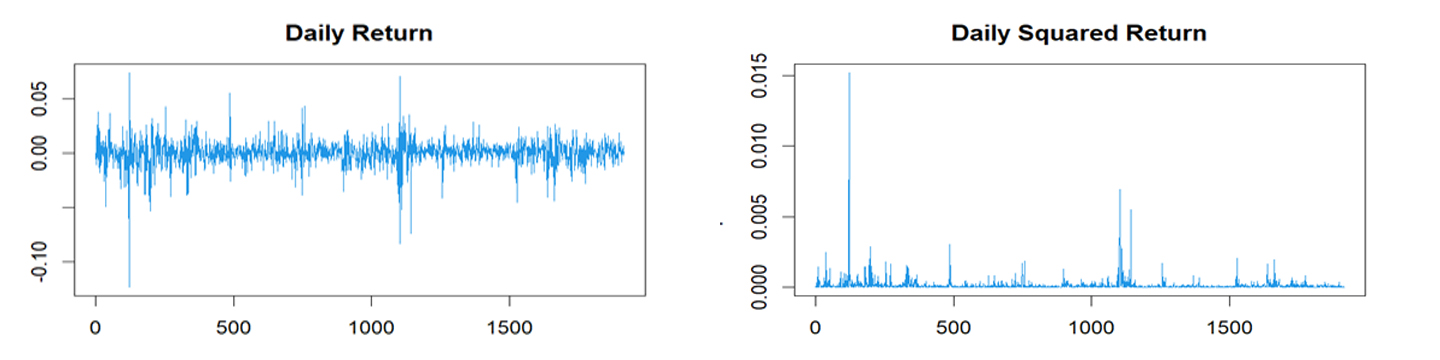
نلاحظ من خلال الشكل (4) عدم وجود ارتباط ذاتي وارتباط ذاتي جزئي في سلسلة العائدات اليومية، حيث يتبين عدم وجود (5%) من النقاط خارج حدود الثقة (95%)، على الرغم من عدم انقطاع السلسلة الزمنية للعائد باتجاه الصفر بعد الفجوة الأولى مباشرة وانما اخذت شكل دالة الجيب في تموجها حول خط الوسط، كما يبين الشكل (5) وجود ارتباط ذاتي في مربع سلسلة العائد لوجود (30%) من النقاط خارج حدود الثقة واخذت شكل الدالة الاسية في انحدارها نحو الصفر ، وعدم وجود ارتباط ذاتي جزئي في مربع سلسلة العائدات اليومية واخذت شكل دالة الجيب في تموجها، كما يبين الشكل (6) وجود الارتباط الذاتي لكون سلسة العائد ومربع سلسلة العائد غير ناعمة، مما يشير الى وجود ارتباط ذاتي في مربع سلسلة عائدات المؤشر السعودي العام.

جدول (2) اختبار Ljung-Box لسلة العائد اليومي ومربع العائد اليومي للمؤشر العام السعودي

TASI.SR Chi.squared statistic p-value
Log-return 433.76 0.0000
Squared Log-return 121.45 0.0000

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

من خلال الجدول (2) الذي يبين اختبار Ljung-Box لكل من سلسلة العائد ومربع سلسلة العائد، حيث تم رفض الفرضية الصفرية لاختبار Ljung-Box لكل من سلسلة العائد ومربع سلسلة العائد، مما يشير إلى أن السلسلة غير متجانسة شرطيًا والتي تتحقق من خلال استخدام اختبار ARCH، مما يؤكد الحاجة الى منهجية GARCH في دراسة سلسلة عائدات المؤشر العام لسوق الأوراق المالية السعودي.

ثانيا: تقدير النماذج

تم تقدير كل من نموذج EGARCH (1,1) ونموذج GJR-GARCH (1,1) باستخدام طريقة الإمكان الأعظم وباستخدام البوتستراب كما يلي:

  1. تقدير نموذج EGARCH

بناء على دالة الاختبار الذاتي والاختبار الذاتي الجزئي تم تحديد رتبة النموذج، وتمت عملية تقدير نموذج EGARCH (1,1) بناء على التوزيع الطبيعي EGARCH (1,1) -N وتوزيع t، EGARCH (1,1) -T، باستخدام طريقة الإمكان الأعظم وطريقة البوتستراب، وكانت نتيجة التقدير مبينة في الجدول (3)

جدول (3)

نتائج تقدير نموذج EGARCH باستخدام طريقة الإمكان الأعظم وطريقة البوتستراب

المعلمة طريقة الإمكان الاعظم طريقة البوتستراب
Normal Student’s t Normal Student’s t
0.0004

(0.002)

 0.0007

(0.000)

 0.0009

(0.000)

 0.0011

(0.000)
0.3729-

(0.000)

 0.3734-

(0.000)

 0.3821-

(0.000)

 0.3937-

(0.000)
0.1216-

(0.003)

 0.110-

(0.000)

 0.1305-

(0.000)

 0.1416-

(0.000)
0.9585

(0.000)

 0.9603

(0.000)

 0.9611

(0.000)

 0.9701

(0.000)
0.2174-

(0.000)

 0.1880-

(0.000)

 0.2232-

(0.000)

 0.2439-

(0.000)
— 4.910

(0.000)

 — 4.961

(0.000)
Information Criteria معايير المعلومات
AIC -6.4092 -6.5123 -6.5416 -6.6671
BIC -6.3946 -6.4949 -6.6241 -6.6210
H-Q 6.4038- -6.5059 6.5399- -6.7011
Shibata -6.4092 -6.5124 -6.5153 -6.6947
Log Likelihood 6141.7 6241.6 6196.8 6326.4

المصدر: اعداد الباحث باستخدام لغة R

من خلال الجدول (3) نلاحظ ان:

  1. نموذج EGARCH المقدر بطريقة الإمكان الأعظم والمبني على توزيع T له مؤشرات أفضل من نموذج EGARCH المقدر وفق التوزيع الطبيعي، حيث كانت للنموذج المقدر وفق توزيع T اقل القيم لمعايير المعلومات (اكياك، وشوارتز، هنان، وشيبات)، وهذا يدعم الاختبارات السابقة التي أظهرت بان شكل التوزيع لبيانات العائد أكثر جرسية وذات ذيول ثخينة، ونلاحظ ان المؤشر العام السعودي يتأثر بالأخبار السيئة والاخبار الموجبة(يتعرض لأثر الصدمات)، أو ما يعرف بأثر الرافعة المالية، وهذا ما اظهره معامل الرافعة γ في النموذج، حيث كانت قيمة معامل الرافعة سالبة للنماذج المقدرة (EGARCH-N، EGARCH-T ، bootstrap-EGARCH-N، bootstrap-EGARCH-T) وبقيمة ( 0.2174-، 0.1880-، 0.2232-، 0.2439-) للنماذج على التوالي، ومعنوية عند مستوى (0.05، 0.01)، ويشير ذلك الى أن الأخبار السيئة )الصدمات السالبة) تُولد تقلبات أكثر من الصدمات الموجبة (الأخبار الجيدة)، بحيث يكون التباين اللاحق للفترة التي تعرضت لصدمة سالبة أكبر منه في حالة التبيان اللاحق في الصدمة الموجبة، كما نلاحظ أن قيم معامل في النماذج الأربعة قريبة من الواحد حيث بلغت (0.9585، 0.9603، 0.9611، 0.9701) للنماذج على التوالي ويشير ذلك الى وجود تأثير كبير جدا للصدمات، أي أن هناك استمرارية في صدمات التقلب في المؤشر العام السعودي في المستقبل.
  2. نموذج EGARCH المقدر بطريقة البوتستراب والمبني على توزيع T له مؤشرات أفضل من نموذج EGARCH المقدر وفق التوزيع الطبيعي، حيث كان للنموذج المقدر وفق توزيع T اقل القيم لمعايير المعلومات (اكياك، وشوارتز، هنان، وشيبات)، وهذا يشير الى افضلية البوتستراب في تقدير نموذج (EGARCH) سواء بتوزيع T او بالتوزيع الطبيعي، والاشكال (7)، (8) تبين التباين الشرطي لمعالم تقدير النموذج

شكل (7) التباين اشرطي لمعالم تقدير نموذج EGARCH-N

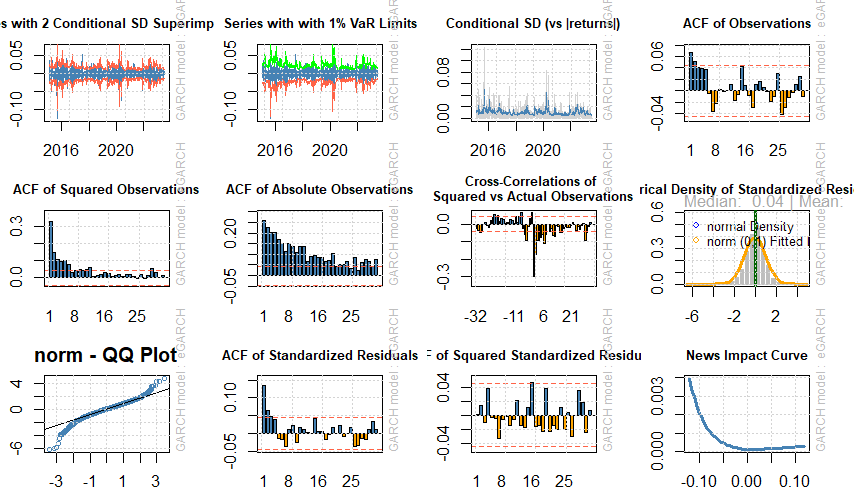
شكل (8) التباين الشرطي لمعالم تقدير نموذج EGARCH-T

  1. تقدير نموذج GJR-GARCH

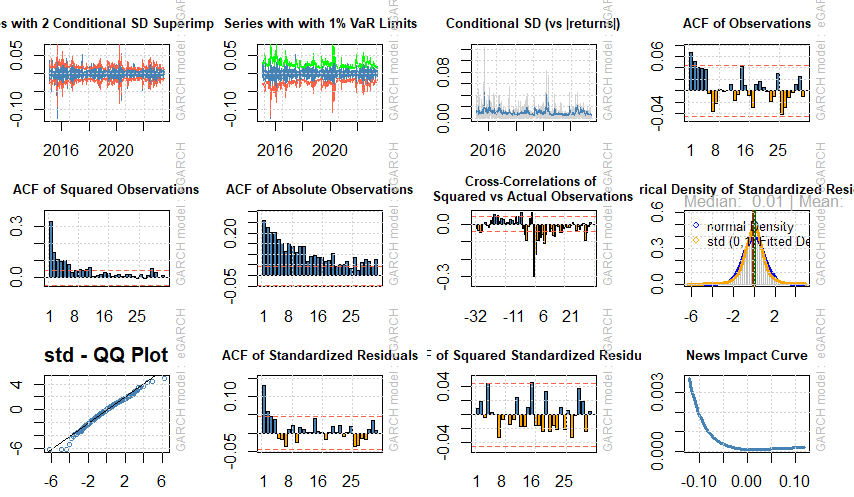
تم تحديد رتبة النموذج بناء على دالة الاختبار الذاتي والاختبار الذاتي الجزئي وشكل الفجوة، وتم تقدير نموذج GJR-GARCH (1,1) بناء على التوزيع الطبيعي وتوزيع t، وباستخدام طريقة الإمكان الأعظم وطريقة البوتستراب، وكانت نتيجة التقدير مبينة في الجدول (4)

جدول (4) نتائج تقدير نموذج GJR-GARCH باستخدام طريقة الإمكان الأعظم وطريقة البوتستراب

المعلمة طريقة الإمكان الاعظم طريقة البوتستراب
Normal Student’s t Normal Student’s t
0.0005

(0.000)

 0.0007

(0.000)

 0.0007

(0.000)

 0.0013

(0.000)
0.000004

(0.000)

 0.000004

(0.000)

 0.000005

(0.000)

 0.00007

(0.000)
0.0466

(0.000)

 0.0261

(0.000)

 0.0298

(0.000)

 0.0301

(0.000)
0.8353

(0.000)

 0.8525

(0.000)

 0.8422

(0.000)

 0.8719

(0.000)
0.1730

(0.000)

 0.1592

(0.000)

 0.1658

(0.000)

 0.1697

(0.000)
== 4.819

(0.000)

 == 4.723

(0.000)
Information Criteria معايير المعلومات
AIC -6.3984 -6.5053 -6.4366 -6.6991
BIC -6.3839 -6.4879 -6.5231 -6.6315
H-Q -6.3930 -6.4989 -6.5511 -6.7109
Shibata -6.3984 -6.5053 -6.5079 -6.6991
Log Likelihood 6131.5 6234.8 6216.8 6324.7

المصدر: اعداد الباحث باستخدام لغة R

من خلال الجدول (4) نلاحظ ان:

  1. نموذج GJR-GARCH المقدر بطريقة الإمكان الأعظم والمبني على توزيع T له مؤشرات أفضل من نموذج GJR-GARCH المقدر وفق التوزيع الطبيعي، حيث كان للنموذج المقدر وفق توزيع T اقل القيم لمعايير المعلومات (اكياك، وشوارتز، هنان، وشيبات)، وتشير المعاملات المقدرة الى وجود أثر الرافعة المالية في المؤشر العام السعودي حيث كانت قيم معامل الرافعة المالية موجبة وتساوي (0.1730، 0.1592، 0.1658، 0.1697) للنماذج الأربعة على التوالي، كما انها معنوية عند (0.05، 0.01)، مما يشير الى ان المؤشر العام السعودي يتأثر بالأخبار السيئة والاخبار الجيدة، وكانت قيم معامل β في النماذج الأربعة كبيرة حيث بلغت(0.8353، 0.8525، 0.8422، 0.8719) للنماذج على التوالي ويشير ذلك الى وجود تأثير كبير جدا للصدمات، أي أن هناك استمرارية في صدمات التقلب في المؤشر العام السعودي في المستقبل.
  2. نموذج GJR-GARCH المقدر بطريقة البوتستراب والمبني على توزيع T له مؤشرات أفضل من نموذج GJR-GARCH المقدر وفق التوزيع الطبيعي، حيث كان للنموذج المقدر وفق توزيع T اقل القيم لمعايير المعلومات (اكياك، وشوارتز، هنان، وشيبات)، وهذا يعطي افضلية لنماذج GJR-GARCH المقدرة بطريقة البوتستراب عن نماذج GJR-GARCH المقدرة بطريقة الإمكان الأعظم في نمذجة عائدات المؤشر العام للسوق المالية السعودية، كما ان معايير المعلومات للنماذج الثمانية (نماذج EGARCH ، GJR-GARCH) تبين الافضلية لنماذج GJR-GARCH المقدرة بطريقة البوتستراب عن نماذج EGARCH في نمذجة عائدات المؤشر العام للسوق المالية السعودية، والشكل (9)، (10) يبين التباين الشرطي لمعالم تقدير النموذج.

شكل (9)

التباين الشرطي لمعالم تقدير نموذج GJR-GARCH-N

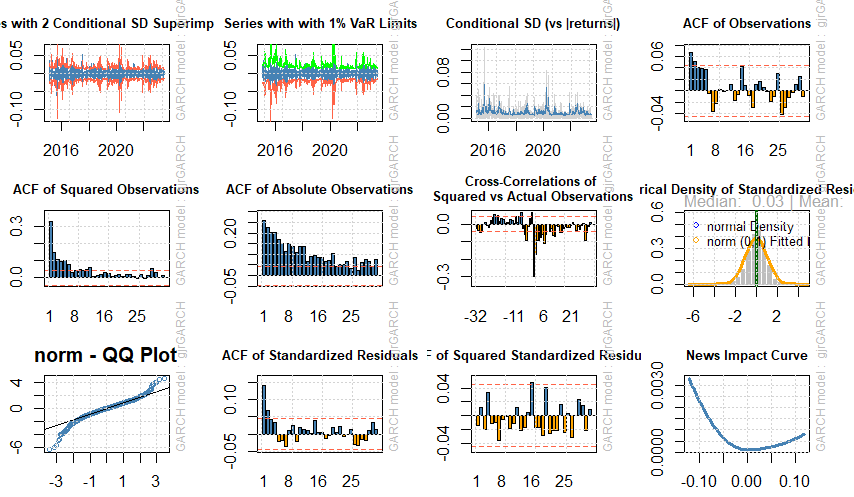
شكل (10) معالم تقدير نموذج GJR-GARCH-T

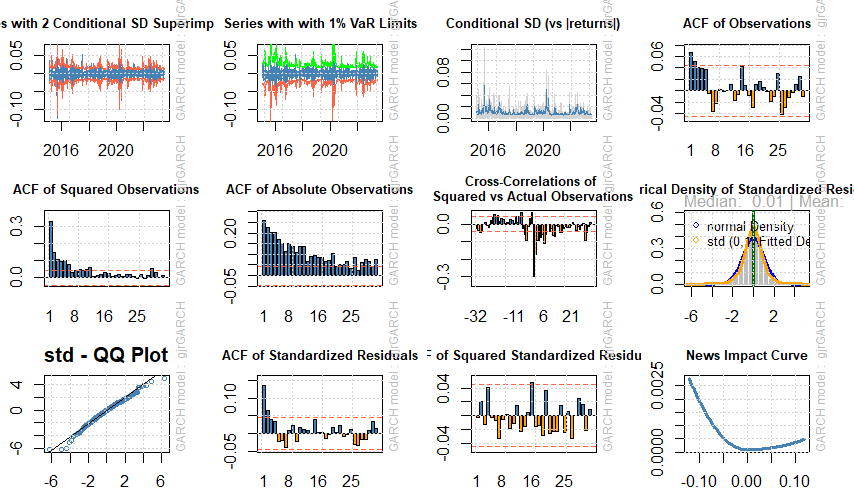
ووفقا لمعايير المفاضلة يعد نموذج GJR-GARCH-T(1,1) المقدر بطريقة البوتستراب هو الأفضل من بين النماذج المقدرة، وبالتالي يعد النموذج GJR-GARCH-T هو الأفضل في التنبؤ بالقيمة المعرضة للخطر للمؤشر العام في سوق الأوراق المالية السعودي.

3- التنبؤ بالقيمة المعرضة للخطر VaR

يعرض هذا الجزء تقدير القيمة المعرضة للخطر للمؤشر العام للسوق المالية السعودية TASI باستخدام النماذج المقدرة، والتنبؤ بها باستخدام نموذج GJR-GARCH التي بينت اختبارات المفاضلة لها انها الأفضل من بين النماذج المقدرة، والجدول (5) يعرض تقدير القيمة المعرضة للخطر عند مستويات ثقة مختلفة (0.90، 0.95، 0.975، 0.99) وباستخدام كل من الطريقة التاريخية ونماذج GARCH المقدرة بطريقة الإمكان الأعظم، ونماذج GARCH المقدرة بطريقة البوتستراب.

ويلاحظ من خلال الجدول (5) بان تقدير القيمة المعرضة للخطر اليومية للمؤشر العام السعودي كانت متباينة وقد تقاربت القيمة التاريخية مع القيم المقدرة بنموذج GJR-GARCH، وبالتالي فان اختبارات التغطية غير المشروطة ستحدد أي التقدير أفضل واي النماذج سيجتاز اختبارات التغطية غير المشروطة.

جدول (5) تقدير القيمة المعرضة للخطر باستخدام طرق مختلفة

النموذج/ الطريقة
-0.03660 -0.02432 -0.01697 -0.01129 التاريخية
طريقة الإمكان الاعظم
-0.02666 -0.02243 -0.01878 -0.01458 EGARCH-N
-0.06596 -0.03695 -0.01935 -0.00610 EGARCH-T
-0.00915 -0.00608 -0.00424 -0.00282 GJR-GARCH-N
-0.03315 -0.02402 -0.01588 -0.01212 GJR-GARCH-T
طريقة البوتستراب
-0.02567 -0.02128 -0.01723 -0.01389 EGARCH-N
-0.06647 -0.03561 -0.01964 -0.01246 EGARCH-T
-0.0207 -0.00772 -0.00610 -0.00387 GJR-GARCH-N
-0.03585 -0.02594 -0.01702 -0.01268 GJR-GARCH-T

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

ثالثا: اختبارات التغطية غير المشروطة

بعد ان تم تقدير القيمة المعرضة لخطر باستخدام نماذج التقدير المختلفة، والى جانب اختبارات المعلومات المستخدمة لاختيار النموذج الأفضل تأتي الاختبارات المستخدمة للقيمة المعرضة للخطر، حيث تم التنبؤ بالقيمة المعرضة للخطر باستخدام النماذج المقدرة، وقد كانت نتائج التنبؤ كما تظهرها الاشكال (11)، (12)، (13)

شكل (11) تقدير القيمة المعرضة للخطر باستخدام نموذج EGARCH عند 99%

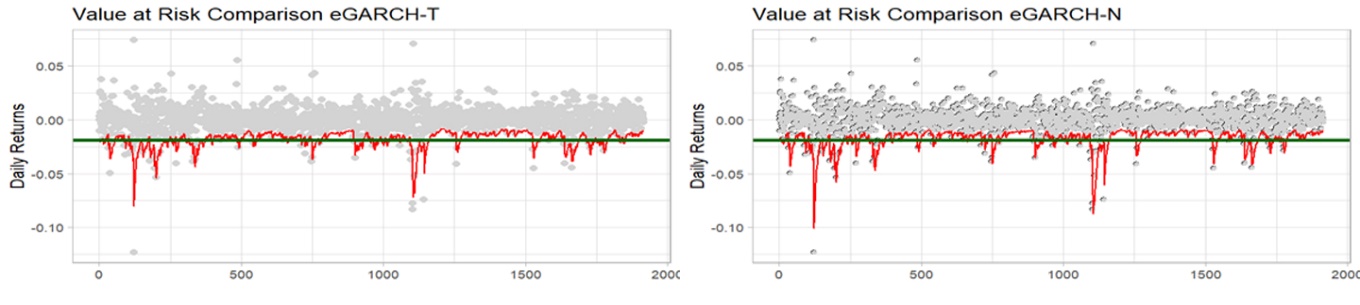
شكل (12) تقدير القيمة المعرضة للخطر باستخدام نموذج GJR-GARCH عند 99%

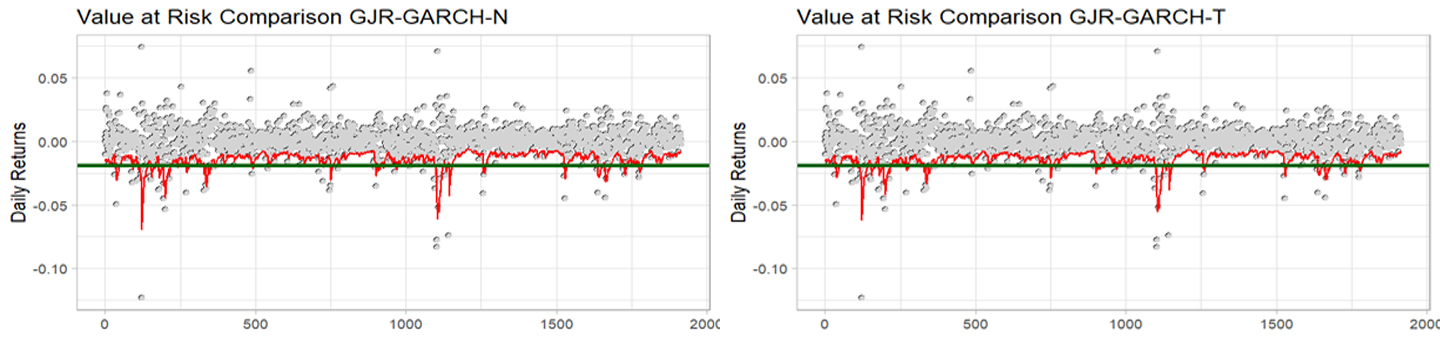
شكل (13) تقدير القيمة المعرضة للخطر باستخدام طريقة البوتستراب لنموذج GJR-GARCH عند 99%

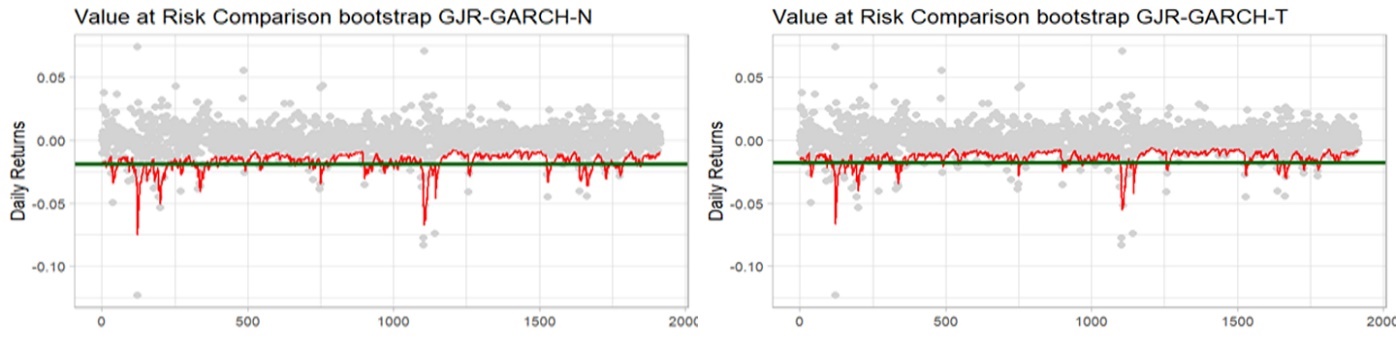
والجدول (6) يبين نتيجة اختبارات القيمة المعرضة للخطر (اختبار VR، اختبار ، اختبار ) للمؤشر العام السعودي عند مستوى (0.01) ومقارنتها احصائيا بقيمة مربع كاي.

جدول (6) اختبارات التغطية المشروطة للقيمة المعرضة للخطر باستخدام النماذج المختلفة 99%

اختبار VR اختبار النموذج
1.47 3.9756 3.9576 EGARCH-N
1.41 4.2614 4.1101 EGARCH-T
1.32 4.1470 4.14213 GJR-GARCH-N
1.25 4.5547 4.7786 GJR-GARCH-T
1.01 5.1128 5.1721 bootstrap GJR-GARCH-N
0.98 7.3499 7.3928 bootstrap GJR-GARCH-T

من خلال الجدول (6) الذي يبين نتائج اختبار التغطية غير المشروطة للنماذج المختلفة نلاحظ بان كافة النماذج معنوية ومقبولة عند مستوى (0.05) وتتمتع بتغطية غير مشروطة، حيث بلغت قيمة مربع كاي الجدولية عند درجة حرية (1) ومستوى معنوية (0.05) (3.84) بينما قيم اختبارات التغطية غير المشروطة تتجاوز هذه القيمة لكافة النماذج، اما عند مستوى معنوية (0.01) فان كافة النماذج غير مقبولة استثناء نموذج bootstrap GJR-GARCH-T)) الذي حققت فيه قيم الاختبارات المختلفة قيمة تتجاوز قيمة مربع كاي عند درجة حرية (1) ومستوى معنوية (0.01) حيث بلغت (6.63)، وبالتالي فان النموذج bootstrap GJR-GARCH-T)) يتميز بتغطية غير مشروطة، وعليه فان التنبؤ بالقيمة المعرضة للخطر لها تغطية شرطية صحيحة، كما انه يمتلك اقل القيم لمعايير المعلومات المختلفة، وهو النموذج الأفضل في التنبؤ بالقيمة المعرضة للخطر للمؤشر العام السعودي (TASI.SR) في سوق الأوراق المالية، كما يشير اختبار نسبة الخسارة الى ان كافة النماذج تعطي اقل نسبة فشل (خسارة) مقبولة للقيمة المعرضة للخطر ، الا ان نموذج bootstrap GJR-GARCH-T)) كان افضل تلك النماذج حيث يعطي اقل نسبة خسارة، ويعرض الشكل (14) التنبؤ بالقيمة المعرضة للخطر

شكل (14)

التنبؤ بالقيمة المعرضة للخطر باستخدام نموذج bootstrap GJR-GARCH-T

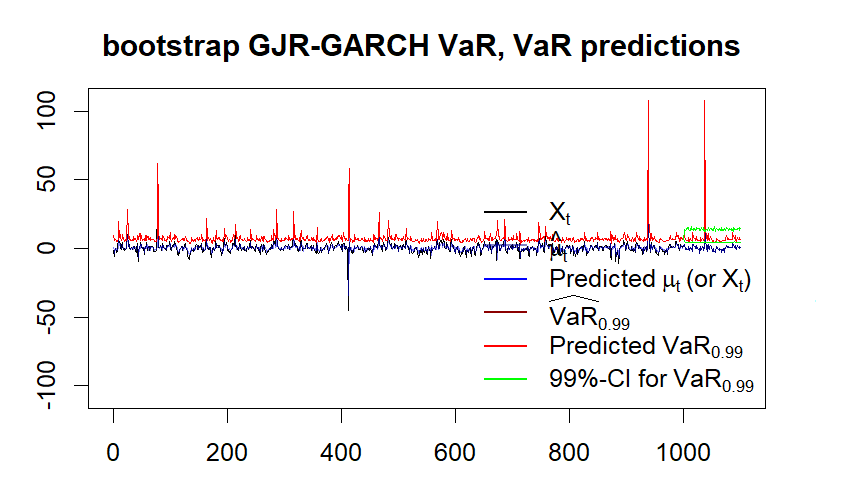
النتائج

من خلال التحليل الخاص بتقدير القيمة المعرضة للخطر للمؤشر العام السعودي توصلت الدراسة الى عدد من النتائج كما يلي:

  1. ان تقلبات عوائد المؤشر العام في سوق السعودية للأوراق المالية لا تتبع التوزيع الطبيعي، مما يشير الى ان استخدام نمذجة GARCH بطريقة البوتستراب تكون أكثر ملائمة.
  2. من خلال اختبارات التغطية غير المشروطة، قدمت النتائج دليلاً لصالح حقيقة أن كافة النماذج مناسبة نسبيًا في نمذجة القيمة المعرضة للخطر للمؤشر العام السعودي TASI عند مستوى ثقة 95%، ويحدث اختلاف واضح في اداء النماذج عندما يكون مستوى الثقة اعلى من 95%، بما في ذلك الطريقة التاريخية في تقدير القيمة المعرضة للخطر.
  3. توصلت الدراسة الى ان النماذج المقدرة وفق توزي T هي أكثر دقة من النماذج المقدرة وفق التوزيع الطبيعي في تقدير القيمة المعرضة للخطر، لذا فإننا نستنتج أن توزيع T يفضل استخدامه عند تقدير القيمة المعرضة للخطر اليومية، لأن الذروة العالية تسمح بمزيد من القيم المتطرفة التي تسجلها سلسلة العائد نتيجة للتقلبات الشرطية.
  4. توصلت الدراسة الى ان نماذج GJR-GARCH هي أفضل من نماذج EGARCH في تقدير القيمة المعرضة للخطر للمؤشر العام السعودي TASI، وبالتالي فان نماذج GJR-GARCH سواء بالتوزيع الطبيعي او وفقا لتوزيع T هي الأفضل.
  5. أظهرت الدراسة ان نماذج GARCH المقدرة بطريقة البوتستراب أفضل من النماذج المقدرة بطريقة الإمكان الأعظم، وهذا ملاحظ ومتوقع كون طريقة البوتستراب تعتمد على البواقي الناتجة من طريقة الإمكان الأعظم او أي طريقة أخرى.
  6. بينت الدراسة ان نموذج bootstrap GJR-GARCH-T هو النموذج الملائم والمناسب لنمذجة القيمة المعرضة للخطر للمؤشر العام السعودي والتنبؤ بها، كونه يمتلك اقل القيم لاختبارات المعلومات.

التوصيات

من خلال النتائج التي توصلت لها الدراسة، توصي الدراسة بالآتي:

  1. توصي الدراسة السوق المالية السعودية باستخدام نموذج GJR-GARCH-T في التنبؤ بالقيمة المعرضة للخطر لما له من قدرة تنبؤية عالية للكشف عن التقلبات والصدمات التي يتعرض لها المؤشر العام السعودي او المؤشرات الفرعية الأخرى.
  2. ضرورة استخدام طريقة البوتستراب في نمذجة التقلبات كطريقة لا معلمية في التنبؤ بالقيمة المعرضة للخطر لكونها طريقة تعطي تنبؤات أكثر دقة وتعطي معلومات قريبة جدا من الواقع.
  3. لكون القيمة المعرضة للخطر مهمة جدا لدى متخذ القرار؛ اذ تشكل مع المخاطر الأخرى معايرة مهمة جدا لأداء الشركة او الشركات المدرجة ضمن المؤشر لذا يجب الاهتمام بالتنبؤ المبني على النمذجة الإحصائية واستخدام الطرق الحديثة ومن ضمنها طريقة البوتستراب.
  4. توصي الدراسة الأسواق المالية المناظرة باستخدام هذه النماذج للتنبؤ بالقيمة المعرضة للخطر فيها.
  5. توصي الدراسة بإجراء دراسات أخرى باستخدام نماذج GARCH الأخرى مثل نموذج IGARCH، ونموذج SGARCH، ونموذج FIGARCH، ونموذج RGARCH، ونموذج AGARCH، ونموذج NAGARCH.

المراجع

  1. عمر، طاهري ومحمد، العقاب، (2022م)، التنبؤ بالقيمة المعرضة للخطر باستخدام نماذج GARCH في ظل وجود مقاطع هيكلية دراسة حالة المؤشر العام لبورصة أبو ظبي (ADX)، مجلة الدراسات المالية والمحاسبية والادارية، مجلد 9، عدد1
  2. David Ardia, Keven Bluteau, Kris Boudt, Leopoldo Catania, (2018), forecasting risk with Markov-switching GARCH models:A large-scale performance study, International Journal of Forecasting,Volume 34, Issue 4,
  3. Algamal, Zakariya Y., And, Resheed, Khairy B., (2010), ” Re – Sampling in Linear Regression Model Using” Jackknife and Bootstrap “, Research Published In The Iraqi Journal Statistical Science.
  4. Martinez, Wendy L, And, Martinez, Angel R.,(2011), ” Computational Statistics Handbook with MATLAB”, United States of America.
  5. Hall, Peter & Yao, Qiwei (2003): Inference in ARCH and GARCH models with heavy-tailed errors, Econometrical, 71(1)
  6. Heinemann, A. M. (2019). Bootstrap inference for conditional risk measures, Doctoral Thesis, Maastricht University.
  7. Naimian, Katayoon, ” (2021). “Application of GARCH Type Models in Forecasting Value at Risk Major
  8. Wu, Chunchou, (2018), Measuring and Comparing the Value-at-Risk Using GARCH and CARR Models for CSI 300 Index, Theoretical Economics Letters , Vol.8 No.6.
  9. Askar Nyssanov , (2013), An empirical study in risk management: estimation of Value at Risk with GARCH family models, Master Thesis in Statistics, Uppsala University, Sweden.
  10. Amiri, Hossein & Nejad, Mahmood Najafi and Mousavi, Seyede Mohadese, (2022), Estimation of Value at Risk (VaR) Based On Levy GARCH Models: Evidence from Tehran Stock Exchange
  11. Hidayana, Rizki Apriva and Subiyanto and , Supian, Sudradjat (2022), The Study of Value-At-Risk Calculation and Back-testing Using the ARMA-GARCH Model Based on Stock Returns: An Overview
  12. Nurhayati, & Wiwin Apriani, and Ariestha W Bustan, (2022), Value At Risk Prediction For The GJR-GARCH Aggregation Modele, Pattimura International Journal of Mathematics, vol 1, NO 1.
  13. Misha Dol, (2021), Comparison of the GARCH, EGARCH, GJR-GARCH and TGARCH model in times of crisis for the S&P500, NASDAQ and Dow-Jones, The Journal of Business.
  14. Christian Francq and Jean-Michel Zakoıan (2010) , GARCH Models Structure, Statistical Inference and Financial Applications , John Wiley & Sons Ltd , France