Functional Analysis and Fixed Point Evaluation with Vector Spaces

Lecturer, Ansam Ghazi Nsaif¹

Faculty of Basic Education, University of Wassit, Iraq

E mail: ansaif@uowasit.edu.iq

HNSJ, 2022, 3(2); https://doi.org/10.53796/hnsj324

Download

Published at 01/02/2022 Accepted at 12/01/2022

Abstract

Functional analysis and fixed point based evaluation is associated with the field of mathematical analysis, which is concerned with and the norm-related vectors and linear functions of vector spaces. Most of functional analysis’s conceptual history goes back to the formulation of continuous, unitary, and also Fourier-analytic functions as operators between spaces. A system of partial differential and numerical solutions gave valuable results in this regard. In a functional analysis, several spaces have dimensions that go on forever. For 2-D and 3-D cases, it might be necessary to provide an explicit context for such spaces. However, functional theory relies on a very different thought process. Rather important theorems typically use the axiom of choice, but it is important to first be able to deduce the Hahn–Banach theorem in all cases where the axiom of choice is unnecessary, since it may not always be strict.

Key Words: Fixed Point, Functional Analysis, Vector Spaces

1.1 Introduction

The application of the use of the term functional as just a noun is found in calculus: it refers to a function, one that is represented by a function [1]. When in the book industry, I will work two weeks and have a complete turnaround [2]. But in real life, if you want anything done it would take a lifetime. Hadamard’s nonlinear approach was followed up by other students, such as Lévy. The modern school of linear functional analysis developed by his mentor, the Banach family, and others was greatly influenced by the fact that Stefan Banach was Jewish [3].

The topic is now viewed as linear functions endowed with the architecture in special cases with infinite-dimensional topologies. In comparison, finite-dimensional spaces are studied often in linear algebra. Often known as measure integration, infinite dimensional analysis, this analysis is an extension of the concepts of measure, function, integration, and probability to an infinite space [4, 5].

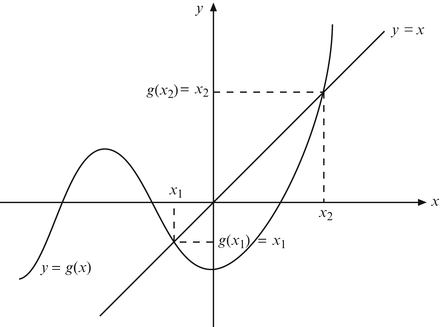
Figure 1: Fixed Point based Plot

Prior to the discovery of closed-normed vector spaces, the simple and first-order spaces to be analysed in functional analysis are complete real- or complex-valued spaces. Banach spaces are known as regions. Concretely speaking, we might define an essential case study as a Hilbert space [6], where the default emerges from the inner product. Some of these fields, including quantum mechanics, differential equations, and Fourier analysis, absolutely depend on creative spaces [7, 8].

For a wider, more general explanation, Fréchet spaces and topological vector spaces, which are Fréchet spaces without a norm, are used [9, 10].

Studying the Banach and Hilbert continuous operators is vital to the study of continuous functional analysis. C-algebras and other operator algebras go hand in hand [11, 12].

1.2 Invariantangled Hilbert spaces

As there is a special Hilbert space for any cardinality of the unintelligible form, they can be isomorphically be determined [13, 14]. Finite-dimensional Hilbert spaces are homeomorphic to linear spaces, and infinite-dimensional Hilbert spaces are mutually inverse [15]. A crucial issue in applications is separability, and functional analysis generally deals with from this space. Perhaps one of the most controversial open issues in functional analysis is to identify all the invariants of the linear operators on a Hilbert space. Many invariant subspaces have been shown to be well-defined [16].

Banach spaces are a bit more difficult to work with than Hilbert spaces. I would like to point out in particular to Banach spaces that do not have an orthonormal basis. The rest of the analysis is the function space of all coherent maps from the underlying space into itself, a.a.k.a. Banach space In a Banach space, a subspace is obtained by duality. However, in practise, it’s not one-to-one [17]. A Banach space need not be bidimensional in any way, regardless of the number of dimensions. In the dual space essay, you can see how and why this works [18].

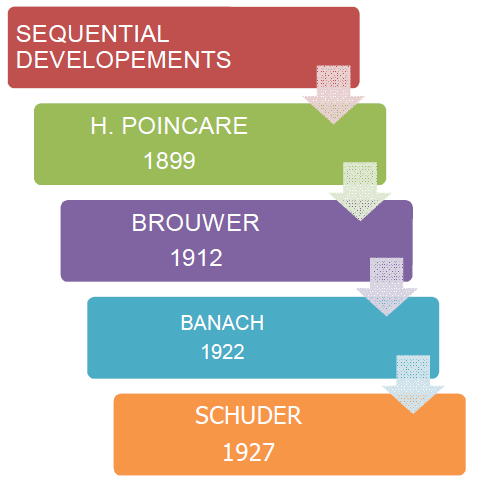
Figure 2: Timeline Factors

Even more generally, the idea of a derivative can be applied to functions between Banach spaces as well [19, 20].

The current state of functional analysis has the following tendencies: Banach spaces have many concepts. one is a combinatorial approach in which numerous combinatorial Banach spaces play a prominent roles; another is about Banach space depictions. Mackey’s ergodic method was established by Connes. Interconnectedness of quantum theory Israel Gelfand: Used mathematically or widely, for representation theory [21, 22].

The spectral theory is used to describe theories that go beyond the single-square eigenvalue and eigenvalue theories. The general solutions of linear equations are used in the analysis of linear algebra. That the theory is related to the proposition that analytic functions of the spectral parameter can be applied to analytic functions. Time slows down in the way that we experience it in creative endeavours, particularly when we are re-creating music and in creating something new music.

Spectral theory was formalised by David Hilbert by way of infinitely many-variate quadratic forms. When formulated in an infinite-dimensional setting, the original spectral theorem is thus considered to be a variant of the theorem on principal axes. Quantum mechanics later turned out to be true when it was found that the concepts from spectroscopy could clarify aspects of atomic spectra. Friedrich said, “I founded my theory of exponentially much variables for pure mathematical reasons, but was unaware that it’d later find applied to physics” [23]

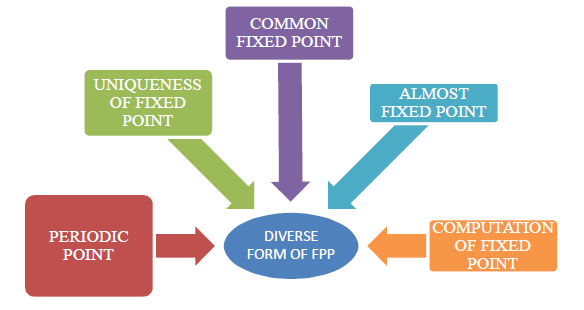
Figure 3: Diverse Forms

1.3 Theorems in Applied Calculus

There are a host of fixed-point statements as well as several more complicated ones. Fixing theorems can be seen in an infinite dimensional vacuum. Fractal compression will create a function for each collage. Iterative design will find the specific function quickly [24, 25].

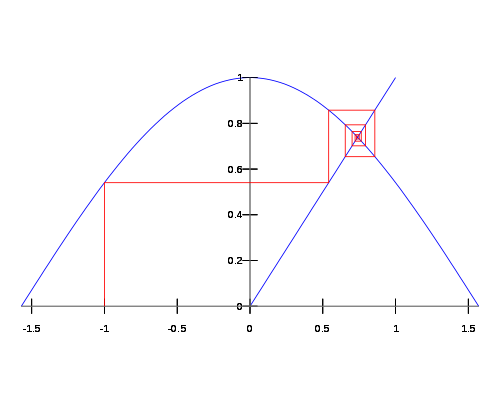
Figure 4: Fixed Point based Plot

The theorem is applicable in the realm of syntax comprehension, and semantics. In lambda calculus, finding a fixed point is an often-noted theme. The common element of all lambda expressions [26, 27] is that they are “recursive functions”, and any fixed-point combinatory takes a lambda expression as input and generates the patterns [28]. From a mathematical point of view, the fix-point theorem is extended to the same function, however, the principle itself will change quite dramatically over time [29].

A computability proof can also has the same statement of the definition be given by using Kleene’s recursion. Knaaster–theorem T’s is not a weak that what denotational semantics uses as an example [30].

Even with regard to the Church–Turing thesis in mind, though, a recursive functions would be completely arbitrary; they can be arbitrarily defined as the least fixed points of their Church-T computation feature [31].

Standard functions defined over all ordinals would have at least one (and indeed only one) one fixed point [32]. Any poset has its “closed components”, and these are the key reason for the existence of the closure operator [33].

Figure 5: Brouwer Fixed Point Theorem

1.3.1 Theorems on Fixed-Point

• Ryll-Nardzewski approach
• Kakutani approach
• Browder approach
• Knaster–Tarski theorem
• Poincaré–Birkhoff theorem proves the existence of two fixed points
• Fixed-point property
• Diagonal lemma
• Schauder approach
• Kleene approach
• Brouwer approach
• Topological degree theory
• Fixed-point lemma for normal functions
• Borel approach
• Caristi approach
• Nielsen approach
• Atiyah–Bott approach
• Brouwer Fixed Point Theorem
• Banach approach
• Tychonoff approach
• Lefschetz approach
• Injective metric space

In computability theory, it is possible to derive the same result by applying Kleene’s recursion. The results of this study are not identical theorems; the Knaster–Tarski theorem is a more significant. Though war seems to be popular, it isn’t good for the commonwealth because it brings suffering, and this idea has found its way into society again, creating more and worse wars is very reasonable. “However, on the light of the Church–Turing thesis, the idea of stability or the least fixed point of logical mapping functions has the same significance: a recursive function is the least fixed part of it.”

The method of iterating a method to find a normal point in set theory is the same in ordinals; any continuous function from the integers to the ordinals has (and indeed, each ordinal) a (and also has) a strictly convergent pointwise limit.

Any poset has its points of closure; these are what we mean by being a member of the poset, and those are the major reason the closure operator was created.

For a finite collection of elements, the eigenvalues and the number of fixed points have equal parity. Using these results, he gave a concise statement of Fermat’s theorem, saying that a triple of integers is either congruent to 1 mod 4 or that it has a single fixed representation. Since the number of fixed positions in the first involution was an odd number, so did the second.

Since the Don Zagier observation described one-congruent and two others have two different representations of a given prime, two of them were found to have a fixed point each. Similarly, because the second involution has odd numbers of fixed points, it must still be able to be represented by the even-power of two dimensions [34].

The theory of the existence of spectral phenomena has had been described in three main ways, each applicable to different areas. Many physicists wanted to find a mathematical representation for both mathematical concepts and physical concepts which Hilbert provided in his initial paper. It’s important for designers to examine the differences between goals and objectives in order to choose the appropriate values for research in the process of designing a product, instead of simply copying another. This theory further developed to investigate Banach algebra in general occurs and this derivation takes you into the non-commutative harmonic analysis.

Applying Fourier analysis is easy; the challenge is making the relation. For all practical purposes, the Fourier transformation on the real line is the spectral principle of differentiation. If you have to generalise your results to cover it, you would have to have an entire eigenfunction (for example, by means of a rigged Hilbert space). In contrast, Pontryagin duality captures the continuum of the properties of the Fourier transform.

However, evidence points of operators can also be studied on Banach spaces. Another way to explain this is that compact users on Banach spaces have the same spectrum as matrices.

1.4 Analytics Patterns

The primary purpose of this branch of mathematics is to study functions of functions. The discipline became well known in the 20th century when it was discovered that mathematical processes of diverse purposes, such as algebra and applied calculus, exhibited identical properties. Atomic, like a function, describes a relationship between numbers and things, and things, but not necessarily either a number or a vector. Formations of structures such as these are called “spaces.” Functional is a great because it describes the interaction of two or more functions (its derivative). It may also serve a purpose. Class theory concentrates on functions such as differentiable or commensurable.

Over the complex number numbers, the simple and traditionally earliest types of spaces that functional analysis looks at are complete normed spaces. According to the theorists, such places are labeled Banach spaces. An significant illustration is the inner product space, where its norm exists. In the governing equations of classical physics, machine learning, differential equations, and the Fourier transform, these spaces are invaluable.

Functional research extends beyond normed topological vector spaces and Fréchet spaces and Fréchet spaces of other types as well.

Banach and Hilbert operators are significant in the study of continuous linear functional analysis. These all flow directly to C* and other derivative algebras.

Functional analysis is based on the Hahn–Ban theorem. It extends the concept of linear functions to the subspace of a vector space, and there are plenty to keep us interested in the dual.

Conclusion

Throughout the duration of more than a century, the entire range of problems has proliferated into many areas, as far-difficult to comprehend as the fixed-point representation of mathematics has become. The different formulations of fixed-point theory were first formulated by French mathematician H. Functional analysis and topology are related to a subdiscipline known as the fixed-point principle. Hyperconve’s concept of hyperspacial space was first laid out by Arons and Panitch in 1956 Soardi (1979) demonstrated that nonexpansive fixed points are valid for unbounded hyperconvexes. Since then a variety of exciting projects have come to light. Since Mazurki, Kaski, Knaster, and Kazo proved the well-known KKM theorem in 1929, we know the Mazurka n-complex is true. in the infinite-dimensional topological vector space, Fan derived the KM theorem Had some results about fixed point theorems, and coincidences, then moved on to minimaxine inequalities. Hyperconvection comes from Arons and Panitchiksy (1956). A true absolute hyperconvex (an hypercube embedded isometrically rigid space) was demonstrated. (Lacey, 1965), and Linden (1953) (1974). The nonlinear theory is still in the process of growth. This recent interest in these spaces can be traced to the discovery of the fix point property of non-expansive mappings (Soardi, 1979) Because since that time a number of surprising findings have been found to be valid in hyperconcave cavities

References

1. Aliprantis, C.D., Border, K.C.: Infinite Dimensional Analysis: A Hitchhiker’s Guide, 3rd ed., Springer 2007, ISBN 978-3-540-32696-0. Online doi:10.1007/3-540-29587-9 (by subscription)
2. Bachman, G., Narici, L.: Functional analysis, Academic Press, 1966. (reprint Dover Publications)
3. Banach S. Theory of Linear Operations. Volume 38, North-Holland Mathematical Library, 1987, ISBN 0-444-70184-2
4. Brezis, H.: Analyse Fonctionnelle, Dunod ISBN 978-2-10-004314-9 or ISBN 978-2-10-049336-4
5. Conway, J. B.: A Course in Functional Analysis, 2nd edition, Springer-Verlag, 1994, ISBN 0-387-97245-5
6. Dunford, N. and Schwartz, J.T.: Linear Operators, General Theory, John Wiley & Sons, and other 3 volumes, includes visualization charts
7. Edwards, R. E.: Functional Analysis, Theory and Applications, Hold, Rinehart and Winston, 1965.
8. Eidelman, Yuli, Vitali Milman, and Antonis Tsolomitis: Functional Analysis: An Introduction, American Mathematical Society, 2004.
9. Friedman, A.: Foundations of Modern Analysis, Dover Publications, Paperback Edition, July 21, 2010
10. Giles,J.R.: Introduction to the Analysis of Normed Linear Spaces,Cambridge University Press,2000
11. Hirsch F., Lacombe G. – “Elements of Functional Analysis”, Springer 1999.
12. Hutson, V., Pym, J.S., Cloud M.J.: Applications of Functional Analysis and Operator Theory, 2nd edition, Elsevier Science, 2005, ISBN 0-444-51790-1
13. Kantorovitz, S.,Introduction to Modern Analysis, Oxford University Press,2003,2nd ed.2006.
14. Kolmogorov, A.N and Fomin, S.V.: Elements of the Theory of Functions and Functional Analysis, Dover Publications, 1999
15. Kreyszig, E.: Introductory Functional Analysis with Applications, Wiley, 1989.
16. Lax, P.: Functional Analysis, Wiley-Interscience, 2002, ISBN 0-471-55604-1
17. Lebedev, L.P. and Vorovich, I.I.: Functional Analysis in Mechanics, Springer-Verlag, 2002
18. Michel, Anthony N. and Charles J. Herget: Applied Algebra and Functional Analysis, Dover, 1993.
19. Pietsch, Albrecht: History of Banach spaces and linear operators, Birkhäuser Boston Inc., 2007, ISBN 978-0-8176-4367-6
20. Reed, M., Simon, B.: “Functional Analysis”, Academic Press 1980.
21. Riesz, F. and Sz.-Nagy, B.: Functional Analysis, Dover Publications, 1990
22. Rudin, W.: Functional Analysis, McGraw-Hill Science, 1991
23. Saxe, Karen: Beginning Functional Analysis, Springer, 2001
24. Schechter, M.: Principles of Functional Analysis, AMS, 2nd edition, 2001
25. Shilov, Georgi E.: Elementary Functional Analysis, Dover, 1996.
26. Sobolev, S.L.: Applications of Functional Analysis in Mathematical Physics, AMS, 1963
27. History of the Mathematical Sciences ISBN 978-93-86279-16-3 p. 195
28. Riesz, Frigyes; Szőkefalvi-Nagy, Béla (1990). Functional analysis (Dover ed.). New York: Dover Publications. pp. 195–199. ISBN 978-0-486-66289-3.
29. Hall, B.C. (2013), Quantum Theory for Mathematicians, Springer, p. 147
30. Rudin, Walter (1991). Functional analysis. McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5.
31. Munkres, James (2000), Topology (2nd ed.), Upper Saddle River: Prentice Hall, pp. 163–172, ISBN 0-13-181629-2, p. 171
32. Vogt, D., Meise, R.: Introduction to Functional Analysis, Oxford University Press, 1997.
33. Yosida, K.: Functional Analysis, Springer-Verlag, 6th edition, 1980