استخدام نموذج الترددات الزمنية المختلفة MIDAS في دراسة أثر التقلبات غير المتناظرة لسعر الصرف على معدلات التضخم في الجمهورية اليمنية

فواز حسن احمد القاسمي¹

¹ أستاذ الإحصاء المساعد، كلية العلوم الإدارية، جامعة عدن، اليمن.

بريد الكتروني: fawazkassim20@gmail.com

HNSJ, 2023, 4(8); https://doi.org/10.53796/hnsj4817

Download

تاريخ النشر: 01/08/2023م تاريخ القبول: 25/07/2023م

المستخلص

هدفت الدراسة إلى استخدام نماذج MIDAS لنمذجة اثر تقلبات أسعار صرف الدولار الأسبوعية على معدلات التضخم الشهرية في الجمهورية اليمنية، كما هدفت الدراسة الى تقدير نموذج MIDAS باستخدام دوال الترجيح Step)، PDL Almon lags، Exponential Almon lags، Beta lags، U-MIDAS)، من خلال تطبيقه على البيانات خلال الفترة (2017-2022م)، وقد تم تمثيل تقلبات أسعار الصرف الأسبوعية بحجم (312) مشاهدة، بينما تمثلت تقلبات معدلات التضخم الشهرية بحجم(72) مشاهدة، ومن خلال الدراسة والتحليل تم التوصل الى ان نماذج MIDAS أظهرت تقديرا معنويا لنمذجة سعر الصرف الأسبوعي على معدلات التضخم الشهرية، ومن خلال اختبارات المفاضلة كان نموذج MIDAS BETA LAGS افضل النماذج المقدرة لامتلاكه اقل القيم لمعايير المعلومات.

الكلمات المفتاحية: نموذج MIDAS، أسعار الصرف، معدلات التضخم.

Research title

Using the MIDAS different time frequencies model to study the effect of asymmetric fluctuations in the exchange rate on inflation rates in the Republic of Yemen.

Fawaz Hassan Ahmed Al Qasimi¹

¹ Assistant Professor of Statistics, College of Administrative Sciences, University of Aden, Yemen.

Email: fawazkassim20@gmail.com

HNSJ, 2023, 4(8); https://doi.org/10.53796/hnsj4817

Published at 01/08/2023 Accepted at 25/07/2023

Abstract

The study aimed to use MIDAS models to model the impact of weekly dollar exchange rate fluctuations on monthly inflation rates in the Republic of Yemen. By applying it to the data during the period (2017-2022), the weekly exchange rate fluctuations were represented by (312) observations, while the monthly inflation rate fluctuations were represented by (72) observations. Through the study and analysis, it was concluded that the MIDAS models showed an estimate Significantly, to model the weekly exchange rate on the monthly inflation rates, and through differentiation tests, the MIDAS BETA LAGS model was the best estimated model because it had the lowest values of the information criteria.

Key Words: MIDAS model, exchange rates, inflation rates.

المقدمة

يعد موضوع النمذجة من المواضيع القديمة والحديثة في آن واحد، ونظرا لتجدد الأحداث الاقتصادية وتعقيدها تعقدت معها عملية النمذجة، وظهرت عدد من الشكوك الخطيرة على الأساليب القياسية للتنبؤ الاقتصادي التي فشلت في تقديم لمحة اقتصادية دقيقة وتوقعات لصنع السياسات في وقت الازمات، وفي الواقع ، عادة ما تستند نماذج التنبؤ الاقتصادي القياسي إلى طرق الانحدار التي تسعى إلى تفسير العلاقات الاقتصادية والتنبؤ بها من خلال مجموعة من المعلومات المعاصرة والتاريخية، ومع ذلك، فإن حجم البيانات المتاحة للتنبؤ الاقتصادي ضخم، ومتعدد وخاصة في الدول التي تتبع انظمة معلوماتية دقيقة، إذ يكون الإنجاز المهم هو تحديد مجموعة البيانات واستخراج المعلومات ذات الصلة بالمتغيرات الاقتصادية بالأرقام القياسية، واسعار الصرف، والأسهم وغيرها من هذه المتغيرات فقط هو أمر صعب، فالسلاسل الزمنية المالية والمعبرة عن الاقتصاد الحقيقي ليس لها نفس الخصائص، سواء من حيث تكرار أخذ العينات او من حيث القدرة التنبؤية، لكونها بيانات متقلبة بطبيعتها، وبالتالي يصعب تمييز مدخلاتها التنبؤية الحقيقية من وجهة نظر الاقتصاد الكلي، بالإضافة إلى ذلك، فإن التكرار الزمني للبيانات المالية يكاد يكون مستمرًا ومن ثم يصعب استخدامه في سياق النمذجة الشهرية، لذا تم تطوير اسلوب نمذجة البيانات المختلطة (MIDAS) لتلائم هذه الأغراض، وعلاوة على ذلك أثبتت أنها تتفوق على اساليب النمذجة المختلفة من خلال الجمع بين سلاسل البيانات ذات الترددات المختلفة.

والفكرة الأساسية لنماذج MIDAS بسيطة ولكنها مبتكرة بأسلوب تعتمد عدد من المعاملات تسمح بالتجميع الزمني للبيانات عالية التردد على دالة ذات عدد صغير من المعلمات، ويتم تقديرها كجزء من عملية التقدير بأكملها، ووفقا لنموذج MIDAS فانه يستغل كافة البيانات من اجل زيادة القدرة التنبؤية بالمتغير التابع ذو التردد الادنى.

كما ان علاقة اسعار الصرف بمعدلات التضخم تعد من العلاقات الاقتصادية الشائكة والمتداخلة مع متغيرات اخرى في الاقتصاد الكلي كالاستثمار والانفاق ومعدلات الفائدة ، لذا يصعب تقديرها كون اسعار الصرف عالية التكرار (التقلب)، بينما معدلات التضخم منخفضة التكرار، لذا تركز هذه الدراسة على تقنيات التقدير والاختيار في نماذج التردد المختلفة زمنيا باستخدام البيانات الاسبوعية لأسعار الصرف والبيانات الشهرية لمعدلات التضخم، واختيار النموذج الافضل من بين النماذج المقدرة من خلال الاختبارات ومقارنة التوقعات مع القيم الاصلية الخاصة بمعدلات التضخم، وبغرض تحقيق ما تسعى اليه الدراسة قسمت الى ثلاثة أجزاء الأول تناول الإطار العام للدراسة ويشمل منهجية الدراسة والدراسات السابقة، والثاني تناول الإطار النظري للدراسة، والثالث تناول الجانب التطبيقي، ثم النتائج والتوصيات.

الإطار العام للدراسة

وفي هذا الجزء تتناول الدراسة المنهجية والدراسات السابقة كما يلي:

اولا: منهجية الدراسة

1. مشكلة الدراسة:

تتلخص مشكلة الدراسة في تقدير أثر تقلبات اسعار الصرف المقاسة بترددات زمنية عالية نسبيا (الاسبوع) على معدلات التضخم المقاسة بترددات زمنية متوسطة (شهريا) ، اذ مما لا شك فيه ان تقلبات سعر الصرف تسبب صدمات لمعدلات التضخم، فتكمن المشكلة في ايجاد نموذج لدراسة تلك الصدمات، وتتلخص مشكلة الدراسة بالإجابة على التساؤل التالي:

هل يستطيع نموذج الترددات المختلفة زمنيا MIDAS في دراسة أثر تقلبات سعر الصرف على معدلات التضخم؟

وتتفرع منه التساؤلات الفرعية التالية:

• ما مدى قدرة نماذج MIDAS على ابراز الصدمات الموجبة على معدلات التضخم؟
• ما مدى قدرة نماذج MIDAS على ابراز الصدمات السالبة على معدلات التضخم؟
• هل يوجد أثر ذو دلالة معنوية لتقلبات اسعار الصرف في معدلات التضخم؟
• ما هو النموذج الافضل في تقدير أثر تقلبات سعر الصرف في التضخم؟

1. اهمية الدراسة:

تتمثل اهمية الدراسة في كونها تتناول موضوعا حيويا من الناحية التطبيقية بالإضافة الى تناولها طريقة تقنية حديثة في النمذجة الاحصائية المتمثلة بنموذج الترددات الزمنية المختلفة (MIDAS) الذي بني للدراسات التي لا تتساوى فيها حجم العينة من حيث عدد المشاهدات ومن حيث الزمن، وإمكانية تطبيقه في دراسة أثر تقلبات أسعار الصرف الأسبوعية في معدلات التضخم الشهرية.

1. اهداف الدراسة:

تهدف الدراسة الى:

• نمذجة تقلبات اسعار الصرف الاسبوعية وأثرها في معدلات التضخم.
• تقدير نماذج MIDAS المختلفة وصياغة النماذج.
• تحديد النموذج الافضل من بين النماذج المقدرة.

1. فرضيات الدراسة:

اعتمدت الدراسة على الفرضيات التالية:

الفرضية الاولى: لا تستطيع نماذج MIDAS نمذجة أثر تقلبات اسعار الصرف الاسبوعية في معدلات التضخم الشهرية.

الفرضية الثانية: لا يوجد اثر ذو دلالة معنوية لتقلبات اسعار الصرف على التضخم في الجمهورية اليمنية.

1. منهج الدراسة

لتحقيق اهداف الدراسة واختبار فرضياتها استخدمت الدراسة المنهج الوصفي والمنهج التحليلي، حيث استخدمت المنهج الوصفي في عرض وتوصيف بيانات ومتغيرات الدراسة المتعلقة بأسعار صرف الدولار (YER) ومعدلات التضخم (INF)، واستخدمت المنهج التحليلي لتحليل العلاقة والاثر بين تقلبات اسعار الصرف والتضخم، وقد اعتمدت الدراسة على لغة البرمجة الاحصائية R.

1. حدود الدراسة

تتمثل حدود الدراسة بالفترة (2017-2022م) وتتمثل بسلسلة زمنية شهرية لمعدلات التضخم بواقع (72) مشاهدة، وسلسلة زمنية اسبوعية لأسعار الصرف بواقع (312) مشاهدة.

1. تعريف متغيرات الدراسة

تتمثل متغيرات الدراسة بأسعار صرف الريال اليمني امام الدولار الامريكي، ومعدلات التضخم السائدة كما يلي:

• اسعار الصرف

يتم تعريف سعر الصرف على أنه العملة التي يمكن استبدالها كوحدة من وحدات أخرى من العملة، أو قيمة العملة بعملة أخرى. عندما يتم تداول الأموال في المجتمع أكثر من اللازم، ثم قد يحدث التضخم. التضخم هو زيادة أسعار السلع بشكل متواصل. هذا لا يعني أن أسعار السلع المختلفة ترتفع بنفس الدرجة لكن عندما نشتري سلع أو نستثمر في بلد آخر، فإن ذلك يتطلب أن تحصل على بعض من عملة ذلك البلد لإنجاز هذه الصفقة، وكذلك الحال عندما يقوم الأجانب بشراء المنتج اليمني أو الاستثمار في اليمن مثلاً، فالأمر يتطلب حصولهم على الريال اليمني.

• التضخم

يعرف التضخم بانه عملية زيادة أسعار السلع بشكل مستمر، وهذا لا يعني أن أسعار الأصناف المختلفة ترتفع بنفس النسبة، كما ان الزيادة مرة واحدة ليست تضخمًا، حتى ان كان ارتفاع الأسعار بنسبة كبيرة، ويحدد بعض الاقتصاديين معنى التضخم بناءً على أسبابه والبعض الآخر يشرح بناءً على نتائج التضخم، وتوضح النظرية الكمية أن التضخم هو فائض في كمية العملة السائدة، مما يتسبب في فائض على المستوى العام لقيمة السعر. بينما يعتمد على التأثير، (Agus, 2017, p18)

ثانيا: الدراسات السابقة

تناولت بعض الدراسات الاجنبية استخدام نموذج MIDAS بصوره المختلفة الا ان هناك شحة كبيرة لاستخدام النموذج في الدراسات العربية، وتناولت الدراسة الحالية بعض الدراسات كالتالي:

1. دراسة (Khalaf and et all, 2023 (بعنوان ” “Dynamic panels with MIDAS covariates: Nonlinearity, estimation and fit بعنوان “بيانات البانل الديناميكية في المتغيرات المختلفة زمنيا (MIDAS)، اللاخطية، التقدير والملائمة ” تهدف هذه الدراسة الى استخدام نموذج (MIDAS) في البيانات المختلطة في سياق بيانات البانل، لمعالجة مشكلة معلمة الإزعاج غير المحددة، واقترحت الدراسة يجاد اختبارات المعكوس للتحقق من ملائمة نموذج MIDAS جنبًا إلى جنب مع اختبارات معاملات النموذج، ويتم إجراء التحديد التوضيحي والمحاكاة والتحليلات التجريبية والتقدير باستخدام طريقة العزوم المعممة GMM الديناميكية، واستخدام المحاكاة في تطبيق النموذج لتقلبات اسعار الصرف الشهرية على التحوط والعمق المالي ربع سنوية، وتوصلت الدراسة الى نجاعة الطريقة المقترحة لمقاربات الانكماش.
2. دراسة (Kamolthip,, 2021) بعنوان “ MACROECONOMIC FORECASTING WITH LSTM AND MIXED FREQUENCY TIME SERIES DATA ” وكانت بعنوان ” التنبؤ بالاقتصاد الكلي باستخدام نموذج MIDAS لبيانات السلاسل الزمنية المختلطة ذات الذاكرة الطويلة” يوضح هذا البحث إمكانات الذاكرة طويلة المدى (LSTM) عند التطبيق باستخدام بيانات السلاسل الزمنية للاقتصاد الكلي التي تم أخذ عينات منها عند ترددات مختلفة، وتهدف الدراسة الى كيفية تكييف نموذج LSTM التقليدي مع السلاسل الزمنية التي يتم ملاحظتها عند الترددات المختلطة عند تطبيق نفس نسبة عدم التطابق على بيانات التردد المنخفض ومتغير التردد العالي، لتعميم LSTM على حالة نسب عدم التطابق المتعددة، واعتمدت الدراسة على أخذ العينات المختلطة ، وتم اجراء التنبؤ خارج العينة من خلال محاكاة مونت كارلو والتطبيق التجريبي، وتوصلت الدراسة الى ان نموذج MIDAS يتفوق على النموذج الاعتيادي، كما توصلت الى ان التنبؤ بمعدل نمو ربع سنوي للناتج المحلي الإجمالي الحقيقي التايلاندي باستخدام مجموعة واسعة من مؤشرات الاقتصاد الكلي وفق الترددات الفصلية والشهرية يتفوق نموذج الذاكرة الطويلة المقدر بطريقة U-MIDAS بسهولة على نموذج AR(1) القياسي البسيط.
3. دراسة (Aline, 2019) بعنوان” An econometric Panel-MIDAS model of asset returns in the brazilian stock market” واتت بعنوان ” استخدام نموذج Panel-MIDAS للتنبؤ بعوائد الأصول للسوق المالية البرازيلية” وتهدف الدراسة الى تقديم المواصفات والتقدير والاختبار لنموذج اقتصادي قياسي يهدف إلى التنبؤ بالعوائد الفردية للأوراق المالية المدرجة في سوق الأوراق المالية البرازيلية، وتشمل المتغيرات التوضيحية للنموذج متغيرات الاقتصاد الكلي والمتغيرات الأساسية والسلوكية التي تم أخذ عينات منها عند ترددات مختلفة، ويستخدم النموذج منهجية الانحدار MIDAS ، والتي تدعم تقدير الانحدار مع المتغيرات التي تم أخذ عينات منها عند ترددات مختلفة، وتشمل العينة المؤسسات غير المالية المدرجة في البورصة البرازيلية من عام 2010 إلى عام 2016. وتوصلت الدراسة إلى أن النموذج قوي في التنبؤ بالعوائد الربع سنوية للأسهم الفردية المدرجة في السوق المالية البرازيلية.
4. دراسة LUE and et all, 2022)) بعنوان “ Variable Weights Combination MIDAS Model Based on ELM for Natural Gas Price Forecasting “، واتت بعنوان “استخدام المحاكاة في نموذج MIDAS ذو الأوزان المتغيرة للتنبؤ بأسعار الغاز الطبيعي” هدفت الدراسة الى دمج نموذج انحدار MIDAS مع نموذج المحاكاة بنجاح لتشكيل نموذج جديد للتنبؤ المركب، واستخدمت الدراسة في المحاكاة خوارزمية grey-wolf متعددة الأغراض للجمع بين نتائج MIDAS أحادية المتغير وزيادة تحسين دقة التنبؤ، وفي التحليل التجريبي ، استخدمت الدراسة أسعار العقود الآجلة للغاز الطبيعي الأسبوعية لشركة UK NBP للحصول على تنبؤات دقيقة، وتوصلت الدراسة الى أن دقة التنبؤ الشاملة لنموذج MIDAS الجديد المركب هي 26.35٪ و 8.82٪ و 12.91٪ أعلى من تلك الخاصة بنماذج الانحدار MIDAS المعيارية ونماذج MIDAS المركبة ونماذج MIDAS متعددة المتغيرات على التوالي.
5. دراسة (كفية وزكريا، 2022) بعنوان ” استخدام الترددات الزمنية المختلفة MIDAS في دراسة أثر التضخم على النمو الاقتصادي في الجزائر خلال الفترة 2014-2020م” هدفت الدراسة إلى توضيح تأثير معدلات التضخم ذات التردد الشهري على مؤشر النمو الاقتصادي ذو التردد الربع سنوي في الجزائر خلال الفترة 2020-2014 باستخدام نماذج الانحدار ذات الترددات الزمنية المختلفة MIDAS، وذلك للحصول على نتائج أكثر دقة في دراسة التأثير والتنبؤ من خلال الاستفادة من كامل المعلومات الخاصة بالمتغير ذو التردد المرتفع. وخلصت الدراسة التي تعتبر من أوائل الدراسات المطبقة على مؤشرات الاقتصاد الوطني باستخدام نماذج MIDAS، إلى وجود تأثير موجب لكل 03 أشهر من مؤشر التضخم في ثلاثي واحد من النمو الاقتصادي، واستطعنا التنبؤ بقيم النمو الاقتصادي انطلاقا من مؤشر التضخم ذو التردد المرتفع.
6. دراسة (الجزار والبرماوي، 2022م) بعنوان “ أثر الصدمات غير المتماثلة لسعر الصرف على معدل التضخم باستخدام نموذج NARDL “دراسة تطبيقية على الاقتصاد المصري” تهدف هذه الدراسة الى تقديم أدلة تطبيقية بأن صدمات سعر الصرف على معدل التضخم غير متماثلة، فباستخدام نموذج الانحدار الذاتي ذو الفجوات الموزعة غير الخطي (NARDL) ومن خلال سلاسل زمنية شهرية من شهر يناير 2016 إلى ديسمبر 2020، توصلت الدراسة إلى النتائج الآتية أولاً: أن العلاقة بين سعر الصرف ومعدل التضخم غير خطية، مما يعني أن تأثير صدمات سعر الصرف على معدل التضخم غير متماثلة. ثانياً: أثبتت الدراسة قياسياً بأن معدل التضخم في الأجل القصير يتأثر فقط بالصدمات الإيجابية لسعر الصرف، في حين أنه لا يتأثر بالصدمات السالبة لسعر الصرف، مما يعني أن معدل التضخم يرتفع مع ارتفاعات سعر الصرف، في حين أن انخفاضات سعر الصرف لا تخفض معدل التضخم. ثالثاً: أن تأثير کل من الصدمات الإيجابية والسالبة لسعر الصرف على معدل التضخم في الأجل الطويل غير معنوية. رابعاً: أثبتت الدراسة قياسياً أيضاً ومن خلال المضاعفات الديناميكية بأن التأثير لتغير الصدمات الإيجابية بـ 1% على معدل التضخم أکبر من تأثير تغير الصدمات السالبة بــ1% على معدل التضخم وذلك عند کل مفردة من مفردات عينة الدراسة.

الجانب النظري

في هذا الجانب تم التأطير النظري للدراسة والمتمثلة بنموذج MIDAS وطرق التقدير وعلاقة أسعار الصرف بالتضخم، كما يلي:

اولا: نموذج الترددات المختلفة زمنيا MIDAS

عادة ما تستخدم نماذج الانحدار التقليدية المتغيرات وفق مقياس واحد لها (كافة المتغيرات سنوية او نصف سنوية او شهرية) أي ان لها نفس التردد، وذلك لضمان نفس التكرار، ويقوم الباحثون بجمع بيانات السلاسل الزمنية ومعالجتها، إما بتجميع المشاهدات ذات التردد العالي إلى أدنى تردد متاح أو تقسيم البيانات ذات التردد المنخفض لتتحول إلى أعلى تردد متاح، ويتم تجميع البيانات ذات التكرار الأعلى إلى أقل تكرار عن طريق حساب المتوسط أو بأخذ قيمة تمثيلية (على سبيل المثال ، الشهر الأخير من ربع السنة) ، وقد يتم إتلاف الكثير من المعلومات المفيدة، او تقسيم البيانات ذات التكرار المنخفض الى تكرار اعلى باستخدام طريقة الاوزان (على سبيل المثال، لتحويل البيانات السنوية الى ربع سنوية بإعطاء كل ربع وزن معين). (Claudia, 2013, p2)

واستخدم Chow and Lin في عام (1971) علاقة إحصائية بين متغيرات ذات تردد منخفض ومتغيرات ذات تردد عالي من خلال اشتقاق سلسلة زمنية جديدة عن طريق الانحدار أحادي المتغير والانحدار متعدد المتغيرات، وهذه الطريقة تستخدم لتحقيق الاتساق بين السلاسل الزمنية على نفس المتغيرات المستهدفة التي يتم قياسها عند ترددات مختلفة، وتعد هذه المحاولات للتغلب على اختلاف تكرار البيانات في السلاسل الزمنية كان تكون احداها مقاسة ربع سنوية والأخرى نصف سنوية.

واستخدمت نماذج MIDAS بكثرة في السنوات الأخيرة، حيث تتمتع هذه النماذج بالقدرة على اجراء عملية الانحدار لمتغير ذو تردد منخفض بمتغيرات عالية التردد بشكل ملائم، وغالبًا ما يتم تحديد معايير MIDAS بإحكام وتقليل علاقات الانحدار النموذجية التي تأخذ في الاعتبار متغيرات الاقتصاد الكلي عند ترددات مختلفة، وتعطي نماذج MIDAS قدرات تنبؤية وآنية عالية نظرًا لأنها تستخدم البيانات للمتغيرات كما هي بدون أي تحويل يفقدها جزء من قيمها. (Bhaghoe and et all, 2019, p5)

إن نموذج انحدار MIDAS الأساسي محدد ليحتوي عدد محدود من علاقات الانحدار القياسية التي تحتوي على عمليات أخذ عينات في ترددات مختلفة، اذ تم تصميم الاستجابة للمتغير التوضيحي ذي التردد العالي باستخدام كثيرات حدود ذات الابطاء الزمني الموزع، من اجل التقليل من المعلمات الناتجة عن الفجوات الزمنية لترددات المتغيرات، بالإضافة إلى المشاكل المتعلقة باختيار ترتيب الفجوة. (Claudia, 2013, p5)

اقترح كل من Ghysels و Santa-Clara و Valkanov في (2004) الجمع بين ، وهي عملية ذات تردد منخفض، و ، وهي عملية عالية التردد يتم تسجيل مشاهداتها بعدد مرات منفصلة وثابتة، وفي كل مرة يتم ملاحظة قيمة جديدة لـ ، في معادلة انحدار بسيطة يعبر عنها بالاتي:( Luis, 2018, p2)

وبصورة أكثر دقة

حيث وتمثل متجه ويحتوي كل قيم المقابلة لـ ، و وهي عبارة عن متجه عمودي يحتوي اوزان التردد العالي، وتدخل كل مشاهدة عالية التردد خلال للتردد المنخفض في النموذج الخطي مصحوبة بوزنها المحدد وبعدد m من المتغيرات المستقلة يقابلها وm من الاوزان بالإضافة الى حد الخطأ .

عمليًا، عند تقدير نموذج الانحدار MIDAS أو U-MIDAS، نحتاج إلى معالجة جميع المتغيرات وعند الترددات المختلفة وطول الملاحظات المختلفة، وعملية تحويل متغير التردد العالي إلى متجه منخفض التردد ، ولنفترض أن البيانات الشهرية في الربع الحالي لها قوة تفسيرية، على سبيل المثال، J = 2 (أي عند الفجوة الثانية)، هذا يعني أننا بحاجة إلى نمذجة كمجموعة خطية من المتغيرات ، ، ، ويمكن كتابة النموذج بطريقة المصفوفات على النحو التالي: (Sarun, 2021, p6)

في الواقع، يمكن حل هذا النموذج باستخدام طريقة المربعات الصغرى العادية (OLS) وسنحصل من خلال هذه الطريقة على تقديرات متسقة للمعاملات، ويعرف هذا النموذج بنموذج انحدار MIDAS غير المقيد ويشار له ب(U-MIDAS)..

ولكن في الواقع العملي لاستخدامات نموذج MIDAS يكون المتجه 𝜽، كبير بالنسبة لحجم العينة 𝑇 وعندما يحدث هذا، فإن النموذج يعاني من تكاثر المعلمات، الامر الذي يجعل طريقة المربعات الصغرى الاعتيادية OLS تؤدي إلى تقديرات ضعيفة وبالتالي تنبؤات مزيفة، ونلجأ الى فرض قيود على المعلمات من خلال تقييد معاملات كثيرة الحدود للفجوات عالية التردد وإعادة صياغة كدالة في المعلمات الفائقة q ولها المؤشر الفرعي (يتم وضعها داخل متعددة الحدود ذات التردد المنخفض) بطريقة ، ولكل ويتم إعادة تعريفها على أنها حيث γ متجه تجميعي للمعلمات الفائقة التي تحدد دالة الاوزان ، وبالتالي يصبح النموذج كما يلي:( Khalaf, 2023, p5)

حيث معلمة التأثير للتردد الزمني العالي ذات الاوزان.

ثانيا: تقدير نموذج MIDAS

لتقدير نموذج MIDAS يجب تحديد نوع دالة الاوزان المستخدمة وتحديد فترات الابطاء الزمنية، وتوجد العديد من دوال الترجيح المستخدمة مع نموذج MIDAS، الا اننا سوف نذكر اهم أربعة دوال منها والتي سيتم تقدير نموذج MIDAS وفقها، كما يلي:

• 1. دالة الترجيح التدريجية

وتستخدم في حالة كانت العلاقة بين المتغيرات خطية، وتفترض هذه الدالة أن معاملات الميل في كل من المشاهدات الفردية لـ X متساوية، أي أن كل معاملات الانحدار لكل k أخذ عينات من X هي فريدة من نوعها، ويعطى النموذج بالصورة:( Michelle and et all, 2010, p526)

حيث ان هي معاملات الميل لكل فجوات الابطاء الزمني، L الفجوات الزمنية، وتساوي (0,1,2) في حالة كانت الابطاء الزمني 3، وهكذا بحسب تردد البيانات للمتغير المستقل، وهذه الدالة فيها نوعين من الصعوبات المحتملة يتمثل الأول بنمط معاملات الميل (وبالتالي الأوزان على كل من العينات ذات الفجوات المتوسطة) تكون غير مقيدة، ولكون الترجيح متدرج يكون لدينا اعتقاد سابق، أنه يجب إعطاء وزن أكبر للعينات التي تكون مناظرة للمتغير التابع ، والثاني يتمثل بزيادة معدل أخذ العينات ، m اذ تؤدي معادلة النموذج إلى وجود معلمات كثيرة على سبيل المثال ، البيانات التي تم أخذ عينات منها بتردد شهري للاستخدام في نموذج ربع سنوي مع فجوة واحدة تبقى ، ويكون من السهل التحكم في عدد المعلمات، لكن في المقابل بالنسبة للبيانات التي تم أخذ عينات منها بتردد يومي لاستخدامها في نموذج شهري بفاصل زمني واحد، فإن افتراض ، (كون الشهر عبارة عن 22 يوما في أسواق المال وغيره) ، وهذا يعني أنه يجب تقدير 20 معامل ميل مختلف.

• 1. دالة ترجيح ألمون

وتستخدم مع النماذج التي تكون العلاقة بين المتغيرات وفق دالة الانحدار الذاتي (AR) ولا تستخدم عندما تكون النمذجة للمتغير نفسه كنمذجة الانحدار الذاتي المتوسطات المتحركة، وتستخدم أيضا في حالة ان تكون العلاقة بين المتغيرات غير خطية من الدرجة الثانية والثالثة، وتكون القيود المفروضة على معلمات نموذج MIDAS كما يلي: ( (Ghysels and et all, 2006,p9

حيث p رتبة نموذج المون متعدد الحدود، و معلمة التأثير للتردد الزمني العالي، وتتميز هذه الدالة في كونها تعمل على تقييد المعلمات فتصبح عدد المعاملات المقدرة مساوية لدرجة كثيرة الحدود وليست لحالات الابطاء الزمني وبالتالي تعمل على تقييد المعلمات.

• 1. دالة ترجيح المون الاسية

تحقق معادلة ترجيح ألمون الأسي مستوى عالي للغاية من المرونة في ضبط المعاملات المقدرة وتقييد المعلمات، وبالتالي ضمان مستوى مناسب من المعلمات المقدرة مع الترددات الزمنية العالية والمنخفضة، وتستخدم عندما تكون العلاقة بين المتغيرات غير خطية (اسية)، وبصورة أكثر كفاءة من معادلة ترجيح المون السابقة، ويكون نموذج التقييد على المعلمات وفق الصورة التالية: ( Khalaf, 2023, p8)

حيث Q هي القوة في الدالة الاسي، وتكون هذه الصيغة هي أحد أبسط التمثيلات المناسبة لدالة الترجيح الاسية في MIDAS، وعلى الرغم من أنه لا يوجد شيء يحد من أن تكون Q عالية، إلا أن الدالة تحقق مستوى مناسب جدا عندما Q = 2 ، بالإضافة إلى شكل الترجيح على شكل محدب كما في الشكل(1)

شكل (1)

منحنى ترجيح دالة المون الاسية

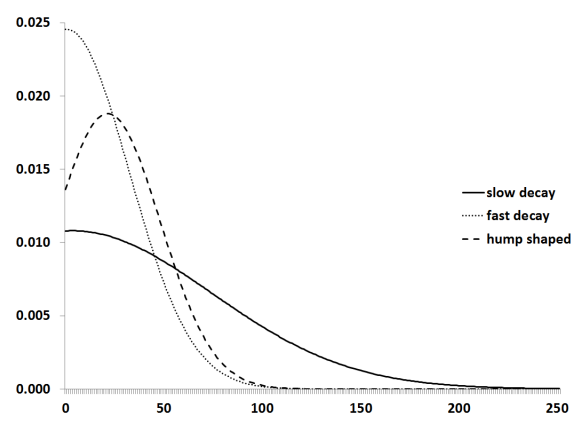
Source: Michelle T. Armesto, Kristie M. Engemann, and Michael T. Owyang,(2010), “Forecasting with Mixed Frequencies,” Federal Reserve Bank of St. Louis Review

وبمجرد تحديد الدالة في النموذج، يعمل معدل الانخفاض على تحديد عدد فترات الابطاء الزمني التي يتم تضمينها في التقدير، ويعتمد في التحديد على البيانات.

• 1. دالة ترجيح بيتا

وتستخدم في حالة كانت البيانات لها سلوك عشوائي او غير متجانسة، وتتطلب دالة ترجيح بيتا طرق تقدير غير خطية وقد تكون مكثفة حسابيا، وتحتوي على معلمتين فقط لكونها تعتمد على توزيع بيتا، ويمكن ان تحتوي على أي عدد من اشكال دالة الترجيح، مع الحفاظ على تقييد المعلمات. (10 Ghysels and et all, 2006,p)

وتعطى صيغة الدالة بالعلاقة التالية: ( Khalaf, 2023, p8)

حيث k عدد محدد من فترات الإبطاء، و معالم الانحدار وفق فترات الابطاء الزمني وفقا لتوزيع بيتا، حيث ، و

وتعتبر هذه الدالة من اهم الدوال المستخدمة وأكثرها دقة لمرونتها العالية مع البيانات عالية التكرار ومنخفضة التكرار وتقييد للمعلمات، والشكل (2) يوضح منحنى دالة ترجيح بيتا.

شكل (2)

منحنى ترجيح دالة بيتا

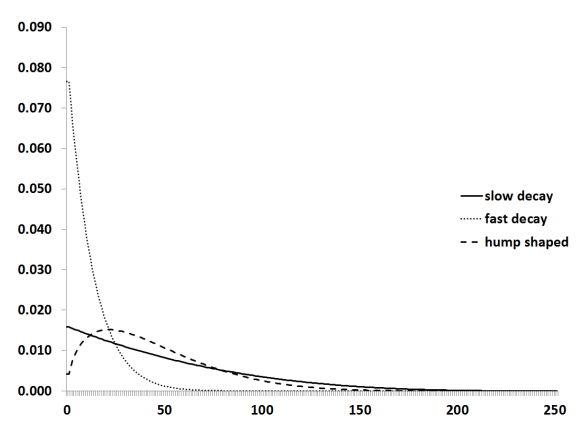
Source: Michelle T. Armesto, Kristie M. Engemann, and Michael T. Owyang,(2010), “Forecasting with Mixed Frequencies,” Federal Reserve Bank of St. Louis Review

الجانب التطبيقي

يتمثل الجانب التطبيقي بوصف متغيرات الدراسة واختبار الاستقرارية وتقدير نماذج MIDAS باستخدام دوال الترجيح المذكورة سابقا، ومقارنة النماذج باستخدام معايير المعلومات، كما يلي:

أولا: التحليل الوصفي

تعتمد الدراسة في الجانب التطبيقي على بيانات أسعار الصرف للدولار مقابل الريال اليمني خلال الفترة (2017-2022م) وهي سلسلة أسبوعية وبواقع (312) مشاهدة، كما تعتمد الدراسة على البيانات الشهرية لمعدلات التضخم خلال نفس الفترة بواقع (72) مشاهدة، أما سلسلة العائد لسعر الصرف وسلسلة العائد للتضخم تم حسابها باستخدام التحويل اللوغاريتمي وفق الصيغة:

حيث ان:

تمثل معدل التضخم عند الزمن t. (سلسلة متوسطة التكرار شهرية)

تمثل معدل التضخم عند الزمن t-1.

سلسلة العائد عند الزمن t.

وبالمثلة تحسب سلسلة العائد لسعر صرف الدولار من الصيغة التالة:

حيث ان:

تمثل سعر صرف الدولار عند الزمن t. (سلسلة عالية التكرار اسبوعية)

تمثل سعر صرف الدولار عند الزمن t-1.

سلسلة العائد عند الزمن t.

1. التمثيل البياني لمتغيرات الدراسة

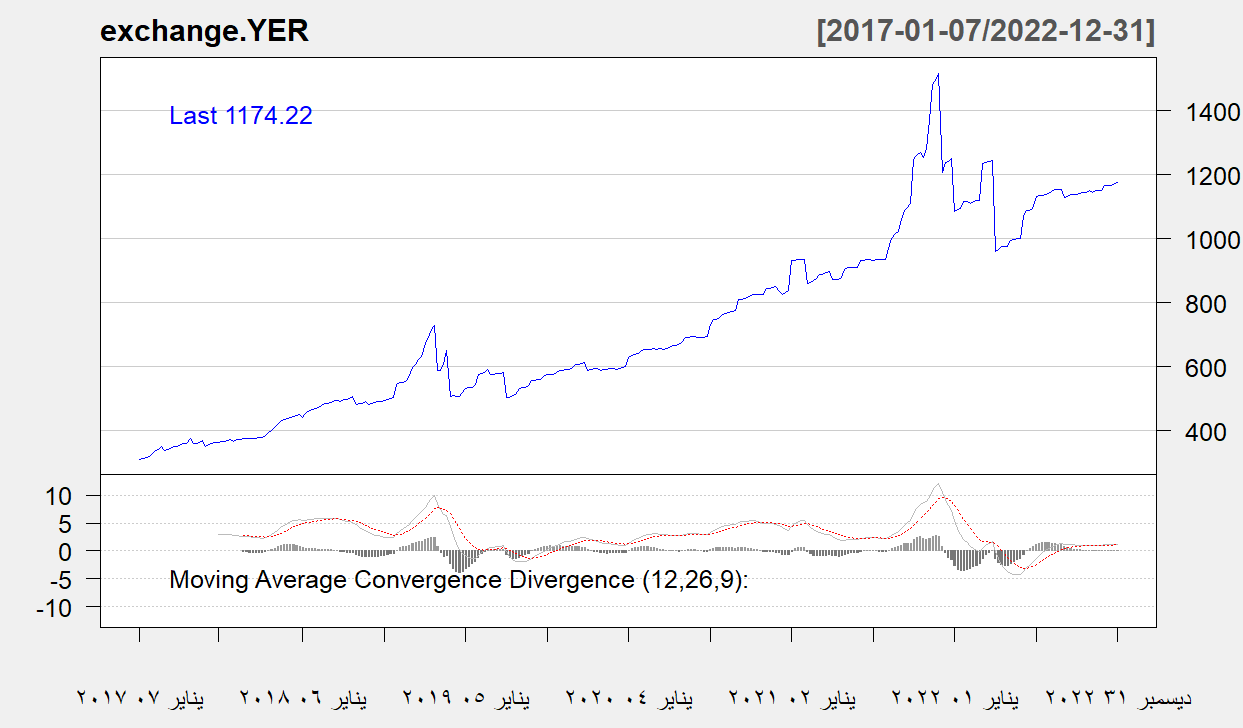
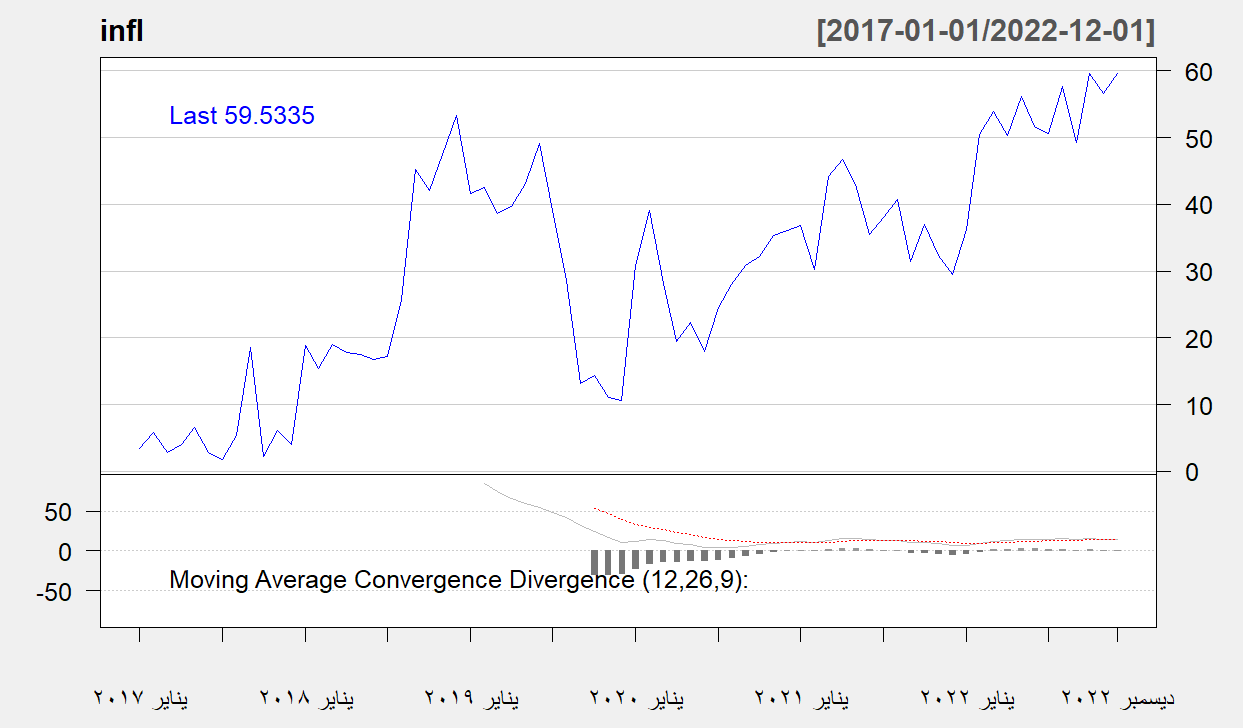
تم ايجاد الرسم البياني لسلسلة سعر صرف الدولار وسلسلة معدلات التضخم مقاسة بمقياسين زمنيين مختلفين حيث قيست سلسلة سعر صرف الدولار بمقياس زمني اسبوعي، بينما قيست سلسلة معدلات التضخم بمقياس زمني شهري خلال الفترة (2017-2022م) ولمعرفة الصورة الاولية لاتجاهات أسعار الصرف ومعدلات التضخم خلال فترة الدراسة، تم تمثيلهما بيانيا، وتم عرضهما في الشكل (3)، (4)

شكل (3)

السلسلة الأسبوعية لأسعار صرف الدولار مقابل الريال اليمني خلال الفترة 2017-2022م

شكل (4)

السلسلة الشهرية لمعدلات التضخم خلال الفترة 2017-2022م

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

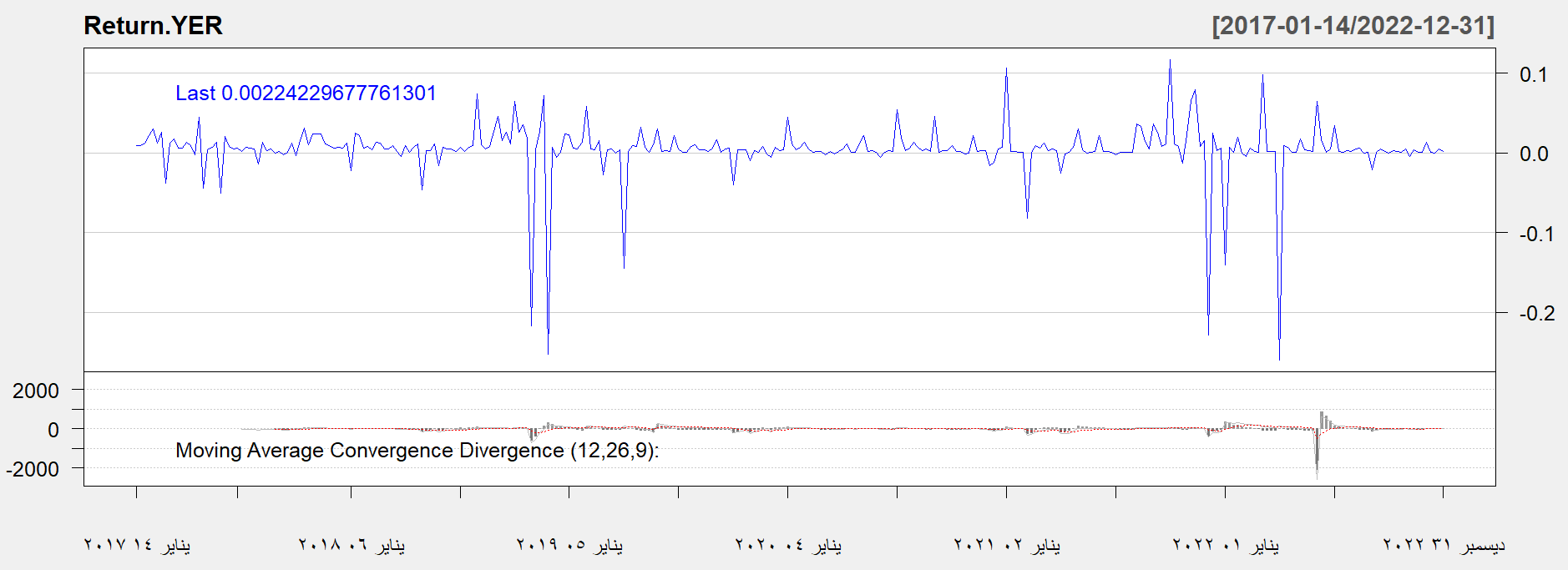
ونلاحظ من خلال الشكل (3) التذبذب والتقلب العالي لأسعار صرف الدولار حيث اخذ اتجاها تصاعديا خلال فترة الدراسة، حيث كان اعلى ارتفاع له في شهر يوليو من عام 2021م، ثم انخفض قليلا وظل محافظا على ارتفاعه بمستوى عالي من التقلب، ويبين شكل المتوسطات المتحركة المبين في ادنى الشكل الى عدم تجانس التباين في سلسلة أسعار الصرف ويوجد انعكاس في المتوسط، كما نلاحظ من خلال الشكل (4) ارتفاع معدل التضخم العام وتصاعده من عام 2018م بمستوى عالي ثم انخفض في منتصف عام 2020م، ثم عاود بالارتفاع ليبلغ اعلى ارتفاع له في شهر يوليو 2021م، ويبين شكل المتوسطات المتحركة ادنى الشكل ان التباين غير متجانس في النصف الأخير من سلسلة معدل التضخم، كما تستخدم السلسلة الأسبوعية لأسعار الصرف والسلسلة الشهرية لمعدلات التضخم في حساب سلسلة العائد لكل منهما باستخدام طريقة حساب العائد ، حيث تم حساب سلسلة العائد وتم تمثيلها بيانيا كما في الشكل (5) والشكل (6)

شكل (5)

سلسلة العائد الأسبوعية لأسعار صرف الدولار امام الريال اليمني

شكل (6)

سلسلة العائد الشهرية لمعدلات التضخم

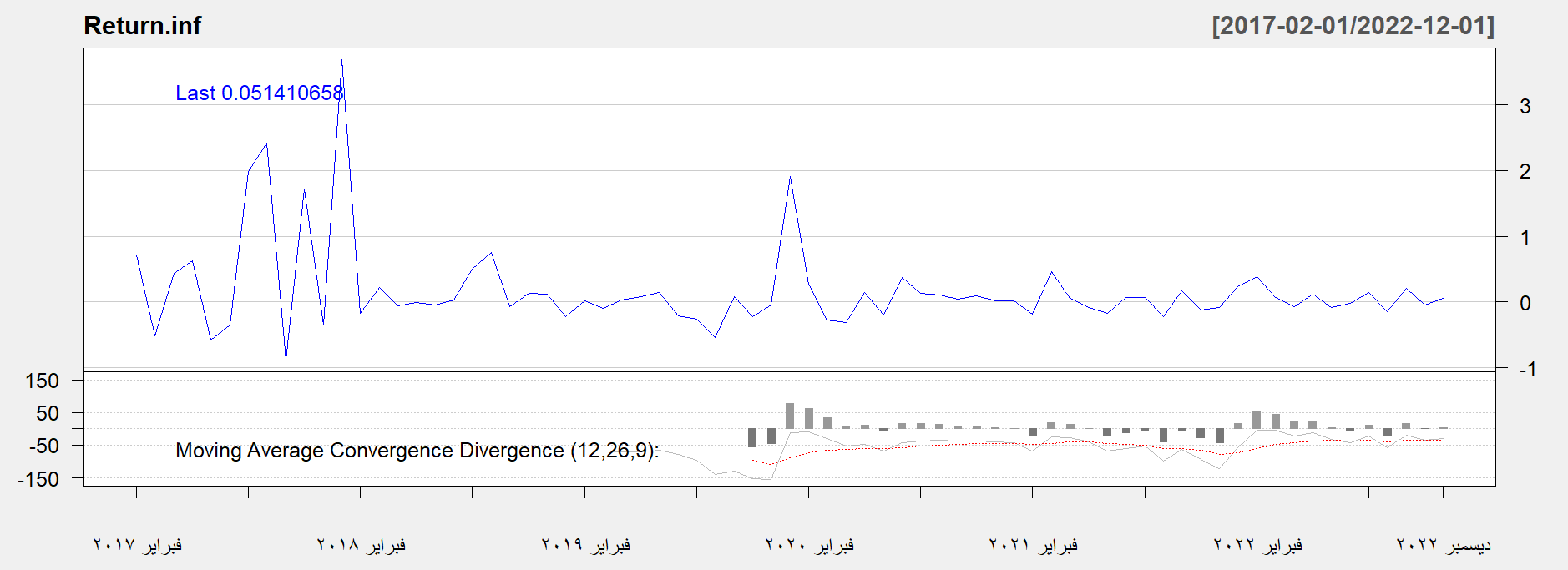
المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

يتبين من خلال شكل سلسلة العائد تقلب أسعار الصرف وكذلك معدلات التضخم ويتضح من خلال شكل المتوسطات المتحركة استقرار سلسلة أسعار الصرف بعد تحويلها الى سلسلة العائد وكذلك بالنسبة لسلسلة العائد لمعدلات التضخم.

1. مقاييس الإحصاء الوصفي للمؤشر

تم استخراج مقاييس الإحصاء الوصفي لسلسة العائد الأسبوعي لأسعار الصرف وسلسلة العائد الشهري لمعدلات التضخم، وتم عرضهما في الجدول (1)

جدول (1)

مقاييس الإحصاء الوصفي لعوائد أسعار الصرف ومعدلات التضخم

JB	Kurtosis	Skewness	Minimum	Maximum	Median	Std.dev	Mean	السلسلة
0.000	27.01	-3.543	-0.2287	0.1236	0.0047	0.0156	0.0049	أسعار الصرف
0.000	13.44	2.96	-0.878	3.681	0.045	0.674	0.1707	معدل التضخم

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

ونلاحظ من خلال الجدول (1) ما يلي:

• 1. ان متوسط العوائد لسلسلة أسعار الصرف قريب من الصفر ويشير إلى ان هناك مجموعة واسعة من التقلبات، كما يشير معامل الالتواء الى ان العوائد غير متماثلة ومنحنية قليلا نحو اليسار مما يشير الى التقلبات السالبة أكبر من التقلبات الموجبة ويعطي مؤشرا مهما حول الصدمات السالبة والموجبة التي تحدثها تقلبات أسعار الصرف في معدلات التضخم، بينما تشير القيمة الإيجابية للتفرطح إلى ان عوائد أسعار الصرف تتبع توزيع الذيول الثخينة مما يشير الى ان غالبية العوائد تتجمع على ذيل التوزيع، والعديد من النقاط العنقودية بعيدًا عن المتوسط.
  2. ان متوسط العوائد لسلسلة معدلات التضخم موجب ولا يقترب من الصفر ويشير إلى ان مجاميع التقلبات غير واسعة، كما يشير معامل الالتواء الى ان عوائد معدلات التضخم لا تتبع التوزيع الطبيعي مما يشير الى التقلبات ملتوية الى اليمين، بينما تشير القيمة الإيجابية للتفرطح إلى ان عوائد معدلات التضخم تتبع توزيع T مما يشير الى ان غالبية العوائد تتجمع على ذيل التوزيع، والعديد من النقاط العنقودية بعيدًا عن المتوسط.

شكل (7) منحنى توزيع سلسلة العائد لأسعار الصرف الاسبوعية

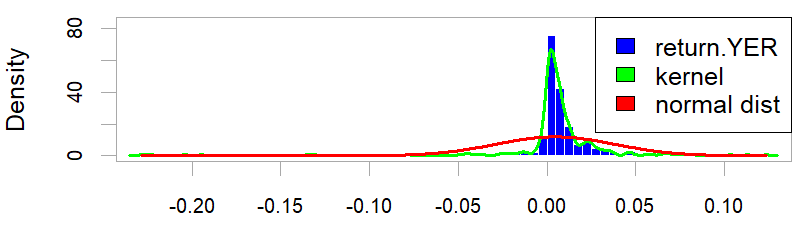
المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

شكل (8)

منحنى توزيع سلسلة العائد لمعدلات التضخم الشهرية

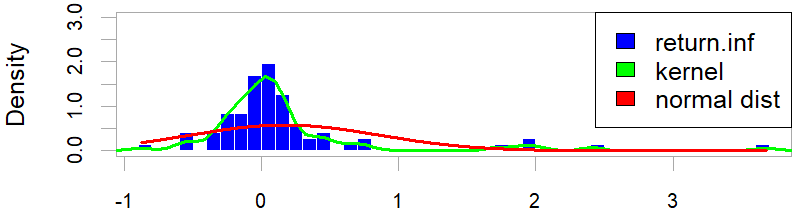
1. اختبار ديكي فولر

لكون المتغيرات المستخدمة في بناء النموذج هما عبارة عن سلسلة العائد لذا فهي مستقرة تماما، الا انها في الغالب تعاني من ارتباط ذاتي، بالإضافة الى وجود أثر للتقلبات او عدم تجانس وثبات حد الخطأ، لذا أجرى الباحث اختبار ديكي فولر الموسع واختبار الارتباط الذاتي والارتباط الذاتي الجزئي لعائد سلسة أسعار الصرف وعائد سلسلة معدلات التضخم، وكانت نتيجة اختبار ديكي فولر كما في الجدول (2)

جدول (2)

نتيجة اختبار ديكي فولر الموسع لسلسلة عائدات أسعار الصرف ومعدلات التضخم

اختبار ADF	مع مقطع		مع مقطع واتجاه		بدون مقطع واتجاه
	قيمة الاختبار	القيمة الاحتمالية	قيمة الاختبار	القيمة الاحتمالية	قيمة الاختبار	القيمة الاحتمالية
سلسلة عائدات أسعار الصرف	18.08-	0.000	18.07-	0.000	17.73-	0.00
سلسلة عائدات معدلات التضخم	5.62-	0.000	6.03-	0.000	5.24-	0.000

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

يلاحظ من الجدول (2) بان سلسلة عائدات أسعار الصرف مستقرة في مستواها وفي الحالات (مع مقطع، مع مقطع واتجاه، بدون مقطع واتجاه) وذلك لكون القيمة الاحتمالية للاختبار والبالغة (0.00) اقل من مستوى المعنوية (١%)، (5%) وهذا يؤدي الى رفض فرضية العدم التي تنص على عدم وجود جذر الوحدة لسلسلة عائدات أسعار الصرف الاسبوعية، كما يتبين من خلال الجدول ذاته استقرار سلسلة عائدات معدلات التضخم في مستواها العام وفي الحالات (مع مقطع، مع مقطع واتجاه، بدون مقطع واتجاه) كانت قيمة مستوى الدلالة (0.00) في الحالات الثلاثة، وهي اقل من مستوى المعنوية (١%)، (5%) وهذا يشير الى رفض فرضية العدم التي تنص على عدم وجود جذر الوحدة لسلسلة عائدات معدلات التضخم الشهرية.

وقد كانت نتائج اختبار الارتباط الذاتي والارتباط الذاتي الجزئي كما يبينهما الشكل (9)، (10).

شكل (9)

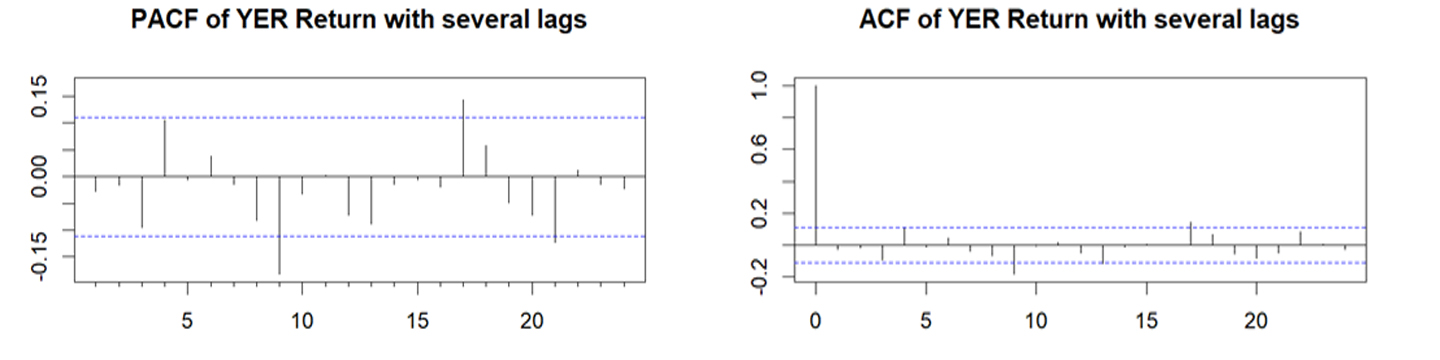
الارتباط الذاتي والارتباط الذاتي الجزئي لسلسلة العائد الأسبوعي لأسعار الصرف

شكل (10)

دالة الارتباط الذاتي والارتباط الذاتي الجزئي لسلسلة العائد الشهري لمعدلات التضخم

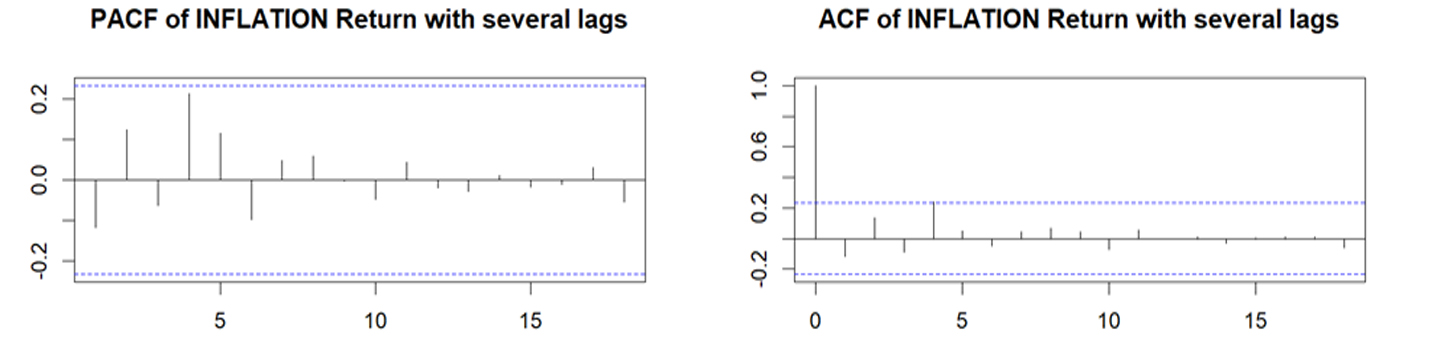
نلاحظ من خلال الشكل (9) وجود ارتباط ذاتي وارتباط ذاتي جزئي في سلسلة العائدات الأسبوعية لأسعار الصرف، حيث يتبين وجود عدد من النقاط خارج حدود الثقة (95%)، وعدم انقطاع السلسلة الزمنية للعائد باتجاه الصفر بعد الفجوة الأولى مباشرة، كما يبين الشكل (10) عدم وجود ارتباط ذاتي جزئي في سلسلة عائدات معدلات التضخم الشهرية لوقوع كافة الفجوات في إطار حدود فترة الثقة، كما لا يوجد ارتباط ذاتي في سلسلة معدلات التضخم، مما يشير الى ان استخدام نموذج MIDASيعد مناسبا كونه يعمل على تقدير النموذج عند فجوات متعددة.

ثانيا: تقدير النماذج

تم تقدير نماذج MIDAS لإيجاد أثر تقلبات أسعار الصرف الأسبوعية على معدلات التضخم الشهرية، وقد تم تقدير النموذج باستخدام الدوال (Step، PDL Almon lags، Exponential Almon lags، Beta lags، U-MIDAS) ، وكانت النتائج كما يبينها الجدول (3)

جدول (3)

نتيجة تقدير نماذج MIDAS في الحالات المتعددة

المعالم	نموذج MIDAS
	U-MIDAS	Beta lags	Exponential Almon lags	PDL Almon lags	MIDAS STEP
الحد الثابت	3.69 0.00	1.24 0.00	1.36 0.00	2.57 0.00	3.44 0.00
الميل	0.38 0.00	0.78 0.00	0.81 0.00	0.36 0.00	0.35 0.00
Lag0		0.04	0.054	0.57	0.001
Lag1		0.01-	0.089	0.42-	0.001
Lag2		0.011-	0.024	0.48-	0.018
Lag3		0.012-	0.079	0.37	0.029
	0.65	0.83	0.82	0.64	0.59
	7.52	6.81	6.83	7.50	7.79
	7.82	6.89	6.99	7.67	7.93
داربن واتسون	1.86	2.01	1.98	1.89	1.81

المصدر: اعداد الباحث باستخدام البرمجة الإحصائية R

من خلال الجدول () نلاحظ بان كافة نماذج MIDAS معنوية واعطت نتائج دقيقة لتقدير تأثير تقلبات أسعار الصرف الأسبوعية على التضخم الشهري خلال الفترة (2017-2022م)، وتبين ما يلي:

1. كان نموذج U-MIDAS معنوي بمعامل ميل (أثر) (0.38) ويشير الى انه كلما تغيرت أسعار الصرف الأسبوعية بمقدار وحدة زيادة واحدة في الأسبوع تودي الى زيادة التضخم بمقدار (38%) من الوحدة ويمتد أثر هذه الزيادة الى شهر كامل، كما بلغت قيمة معامل التحديد () ويشير الى ان (65%) من اجمالي التأثير على معدلات التضخم تعود الى تقلبات أسعار صرف الدولار الاسبوعية، كما تشير قيمة اختبار داربن واتسون الى ان النموذج لا يعاني من مشكلة الارتباط الذاتي حيث بلغت قيمته (1.86) وتقترب من القيمة (2) التي يكون عندها الارتباط الذاتي يساوي الصفر.
2. يشير نموذج Beta lags بان معامل الميل هو (0.78) ويعني ان زيادة أسعار صرف الدولار بوحدة زيادة واحدة تؤدي الى زيادة التضخم بمقدار (78%) من الوحدة، ويمتد أثر هذه الزيادة الى شهر كامل، كما بلغت قيمة معامل التحديد () ويشير الى ان (83%) من اجمالي التأثير على معدلات التضخم تعود الى تقلبات أسعار صرف الدولار وحدها، بينما (17%) من التأثيرات تعود الى عوامل أخرى، ويشير ذلك الى ان التضخم في السنوات التي شملتها الدراسة يتأثر بالصدمات الموجبة لأسعار الصرف فقط والتي تتأثر بالوضع الاقتصادي للبلد، حيث تبين قيم الفجوات بان الصدمة السالبة لسعر الصرف لا تؤثر معنويا على التضخم، بينما الصدمة الموجبة تعمل على زيادة التضخم واستمراره، وتشير الفجوات ايضا (Lag0-Lag3) بان النموذج دقيق جدا في نقل التأثير الأسبوعي الموجب لتقلبات أسعار صرف الدولار الى التضخم الشهري، وان تغير الصدمات من موجبة الى سالبة (تعافي أسعار الصرف) لا تؤثر في الميل ويستمر التضخم كما هو، وتشير قيمة داربن واتسون الى ان النموذج لا يعاني من مشكلة الارتباط الذاتي حيث بلغت قيمته (2.01) وتقترب جدا من القيمة (2) التي يكون عندها الارتباط الذاتي يساوي الصفر، كما ان نموذج Beta lags له اقل القيم لمعايير المعلومات (AIC، BIC) وبالتالي يعد هذا النموذج هو النموذج الأفضل في تقدير العلاقة والاثر والصدمات غير المتناظرة بين أسعار الصرف الأسبوعية ومعدل التضخم الشهري.
3. يشير نموذج Exponential Almon lags MIDAS بان معامل الميل هو (0.81) ويعني ان زيادة أسعار صرف الدولار بوحدة زيادة واحدة يؤدي الى زيادة التضخم بمقدار (81%) من الوحدة، ويمتد أثر هذه الزيادة الى شهر كامل، كما بلغت قيمة معامل التحديد () ويشير الى ان (82%) من اجمالي التأثير على معدلات التضخم تعود الى تقلبات أسعار صرف الدولار وحدها، بينما (18%) من التأثيرات تعود الى عوامل أخرى، في حين تشير الفجوات (Lag0-Lag3) بان النموذج دقيق في نقل التأثير الأسبوعي لتقلبات أسعار صرف الدولار الى التضخم الشهري، الا ان تغير الفجوات يؤثر في قيمة الميل، وتشير قيمة داربن واتسون الى ان النموذج لا يعاني من مشكلة الارتباط الذاتي حيث بلغت قيمته (1.98) وتقترب جدا من القيمة (2) التي يكون عندها الارتباط الذاتي يساوي الصفر، ويأتي النموذج في المرتبة الثانية بعد نموذج MIDAS Beta في دقة التقدير، حيث يمتلك اقل القيم من بقية النماذج الاخرى لمعايير المعلومات (AIC، BIC) .
4. يشير نموذج MIDAS PDL Almon lags بان معامل الميل هو (0.36) ويعني ان زيادة أسعار صرف الدولار بوحدة زيادة واحدة يؤدي الى زيادة التضخم بمقدار (36%) من الوحدة، ويمتد أثر هذه الزيادة الى شهر كامل، كما بلغت قيمة معامل التحديد () ويشير الى ان (64%) من اجمالي التأثير على معدلات التضخم تعود الى تقلبات أسعار صرف الدولار وحدها، بينما (36%) من التأثيرات تعود الى عوامل أخرى، في حين تشير الفجوات (Lag0-Lag3) بان النموذج اقل دقة في نقل التأثير الأسبوعي لتقلبات أسعار صرف الدولار الى التضخم الشهري، حيث ان تغير الفجوات يؤثر بالنقصان في قيمة الميل، وتشير قيمة داربن واتسون الى ان النموذج لا يعاني من مشكلة الارتباط الذاتي حيث بلغت قيمته (1.89) وتقترب جدا من القيمة (2) التي يكون عندها الارتباط الذاتي يساوي الصفر.
5. يشير نموذج MIDAS STEPبان معامل الميل هو (0.35) ويعني ان زيادة أسعار صرف الدولار بوحدة زيادة واحدة تؤدي الى زيادة التضخم بمقدار (35%) من الوحدة، ويمتد أثر هذه الزيادة الى شهر كامل، كما بلغت قيمة معامل التحديد () ويشير الى ان (59%) من اجمالي التأثير على معدلات التضخم تعود الى تقلبات أسعار صرف الدولار وحدها، بينما (41%) من التأثيرات تعود الى عوامل أخرى، في حين تشير الفجوات (Lag0-Lag3) بان النموذج دقيق في نقل التأثير الأسبوعي لتقلبات أسعار صرف الدولار الى التضخم الشهري، حيث ان تغير الفجوات لا يغير في قيمة الميل، وتشير قيمة داربن واتسون الى ان النموذج لا يعاني من مشكلة الارتباط الذاتي حيث بلغت قيمته (1.81) وتقترب جدا من القيمة (2) التي يكون عندها الارتباط الذاتي يساوي الصفر.

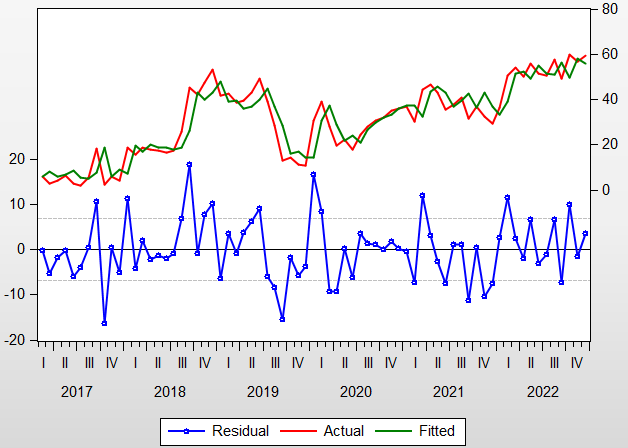
والشكل (11) يبين دقة التقدير من خلال القيم الحقيقية والقيم المقدرة والبواقي باستخدام نموذج BETA

شكل (11)

القيم الحقيقية والقيم المقدرة والبواقي باستخدام نموذج BETA

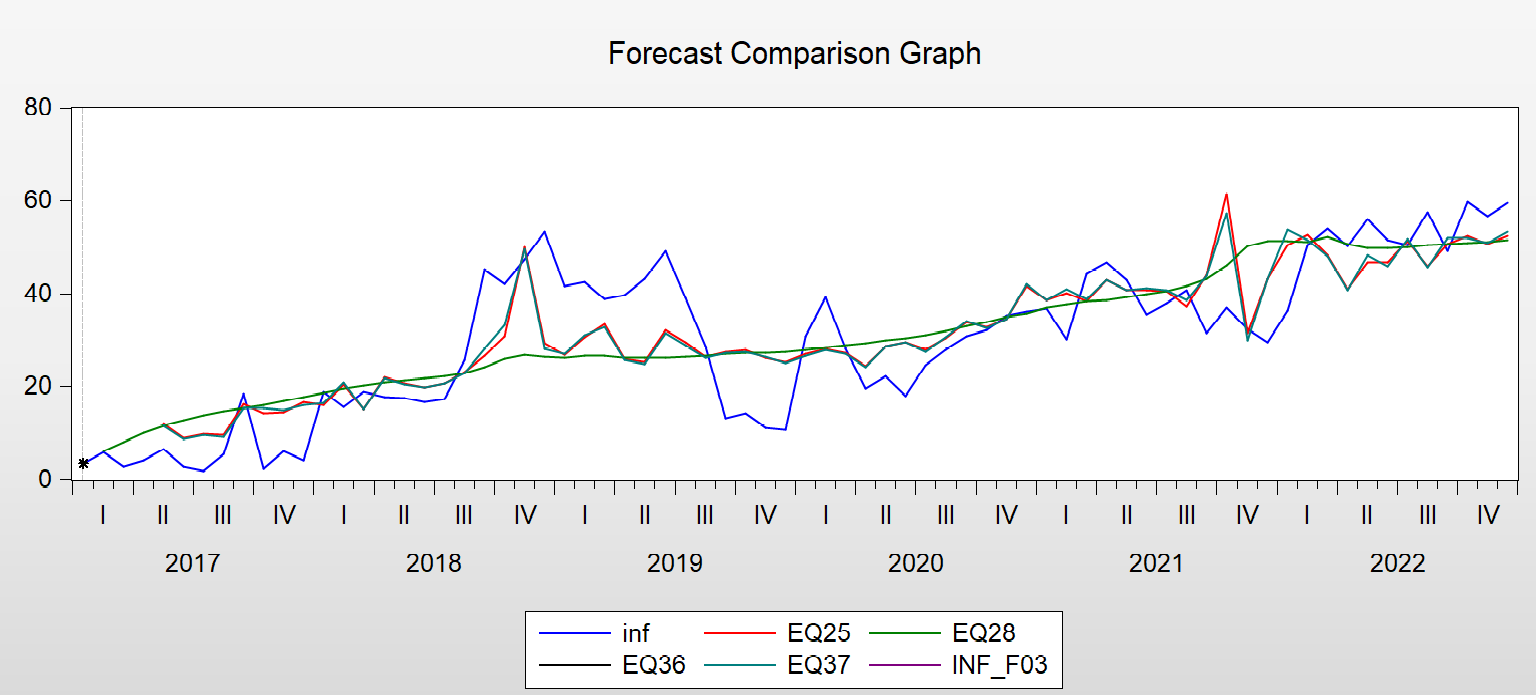
والشكل (12) يعرض التنبؤ بالتضخم الشهري بالاعتماد على أسعار الصرف الاسبوعية

شكل (12)

التنبؤ بالتضخم الشهري بالاعتماد على أسعار الصرف الأسبوعية

النتائج

توصلت الدراسة الى عدد من النتائج هي:

1. توصلت الدراسة الى ان نماذج MIDAS دقيقة ومعنوية في نمذجة الترددات الزمنية المختلفة لأسعار الصرف الأسبوعية ومعدلات التضخم الشهرية.
2. نظرا لعدم توفر البيانات بمقاييس موحدة ودقيقة في الترددات الزمنية بينت نماذج MIDAS أداء تقديري وتنبؤي عالي عندما تكون البيانات غير متوفرة بتردد زمني واحد.
3. ان نموذج MIDAS Beta هو النموذج الأفضل في دراسة تأثير أسعار الصرف الأسبوعية على معدلات التضخم الشهرية، ومع ان الفترة التي شملتها الدراسة تتسم بعدم الاستقرار الاقتصادي في اليمن الا ان النموذج كان دقيقا في تقدير التضخم الشهري من خلال أسعار الصرف الأسبوعية.
4. يعد نموذج Exponential Almon lags MIDAS مناسبا أيضا لتقدير نموذج التضخم حيث اتى في المرتبة الثانية من حيث معايير المعلومات.
5. توصلت الدراسة الى ان معدلات التضخم تتأثر بالصدمات الموجبة فقط أي انه عند زيادة أسعار الصرف تزيد معدلات التضخم، وإذا حدثت صدمة سالبة (تعافي الصرف) يستمر التضخم بالارتفاع ولا يتأثر بالصدمات السالبة مما يشير الى ان الصدمات غير متناظرة والصدمة الموجبة تتبعها استجابة موجبة للتضخم والصدمة السالبة يستمر من خلالها التضخم بالارتفاع.
6. وجود علاقة ارتباط طردية وأثر إيجابي معنوي لتقلبات أسعار الصرف على معدلات التضخم، وتوصلت الدراسة الى انه كلما زاد سعر صرف الدولار مقابل الريال اليمني يؤدي الى زيادة التضخم، والعكس.
7. بينت الدراسة ان معدلات التضخم في اليمن تتأثر بصورة كبيرة جدا بتقلبات أسعار الصرف مع انه في الاقتصادات القوية يحدث العكس كون العلاقة سببية وسببية عكسية، ويعود ذلك الى تعطل السياسة النقدية والمالية للبلد وغالبية مؤشرات الاقتصاد الكلي غير فعالة، مما جعل دور بقية العوامل التي تؤثر على التضخم مساوية للصفر تقريبا نتيجة الأوضاع السياسية والاقتصادية التي تمر بها اليمن.

التوصيات

من خلال النتائج والتحليل توصي الدراسة بالآتي:

1. استخدام نماذج MIDAS في التنبؤ بمعدلات التضخم بناء على تقلبات أسعار الصرف، حيث أظهرت بانها أكثر دقة من النماذج الأخرى. والتي لا يمكن استخدامها في حالة اختلاف التردد الزمني لتكرارات المتغيرات.
2. توصي الدراسة بضرورة استخدام نموذج MIDAS BETA في التنبؤات للمتغيرات ذات التكرارات العالية إذا كانت تكرارات المتغير التابع منخفضة.
3. توصي الدراسة بضرورة تفعيل الاستثمار غير العقاري الذي سيؤدي الى تخفيض معدلات التضخم، حيث اظهر نموذج MIDAS ان تعرض أسعار الصرف لصدمة موجبة تعمل على انتقال التضخم من تكرار عالي (أسبوع) الى تكرار منخفض (شهر) حتى وان عاد سعر الصرف بالانخفاض الا ان التضخم ينتقل لمدة شهر كامل ويتضاعف في حالة تعرضت أسعار الصرف لصدمة موجبة أخرى.
4. توصي الدراسة باستخدام نماذج الترددات الزمنية المختلفة MIDAS في دراسة متغيرات أخرى، وباستخدام نماذج أخرى مثل MIDAS GARCH، MIDAS AR، MIDAS ARDL.

المراجع

1. جرفي، زكريا، (2022)، دراسة أثر سعر صرف الأورو-دينار على الواردات في الجزائر خلال الفترة 2020-2010 باستخدام نموذج الترددات الزمنية المختلفة MIDAS، مجلة ابعاد اقتصادية، المجلد (12)، العدد (1).
2. البرماوى، أدهم والجزار، فاروق. (2022). أثر الصدمات غير المتماثلة لسعر الصرف على معدل التضخم باستخدام نموذج NARDL “دراسة تطبيقية على الاقتصاد المصري”. مجلة کلية الاقتصاد والعلوم السياسية, 23(2),
3. Khalaf, Lynda, Maral Kichian, Charles Saunders, Marcel Voia, (2023), Dynamic panels with MIDAS covariates: Nonlinearity, estimation and fit. Journal of Econometrics, 220 (2).
4. Kamolthip, Sarun, 2021. “Macroeconomic Forecasting with LSTM and Mixed Frequency Time Series Data,” PIER Discussion Papers 165, Puey Ungphakorn Institute for Economic Research.
5. Aline Moura Costa da Silva, (2019), An econometric Panel-MIDAS model of asset returns in the brazilian stock market, GEORGETOWN UNIVERSITY – UNIVERSIA, VOL. 13 NUM. 2.
6. LUE LI, CAIHONG HAN, SHENGWEI YAO, AND LIANGSHUO NING, (2022), Variable Weights Combination MIDAS Model Based on ELM for Natural Gas Price Forecasting, IEEE Access ,Vo: 10.
7. Claudia Foroni and Massimiliano Marcellino, A Survey of Econometric Methods for Mixed-Frequency Data, European University Institute.
8. Bhaghoe, S. & Ooft, G. & Franses, Ph.H.B.F., (2019). “Estimates of quarterly GDP growth using MIDAS regressions,” Econometric Institute Research Papers EI2019-29, Erasmus University Rotterdam, Erasmus School of Economics (ESE), Econometric Institute.
9. Luis Libonatti, (2018), MIDAS Modeling for Core Inflation Forecasting, Cataloging-in-Publication data provided by the Inter-American Development Bank
10. Sarun Kamolthip, 2021. “Macroeconomic Forecasting with LSTM and Mixed Frequency Time Series Data,” PIER Discussion Papers 165, Puey Ungphakorn Institute for Economic Research
11. Michelle T. Armesto, Kristie M. Engemann, and Michael T. Owyang,(2010), “Forecasting with Mixed Frequencies,” Federal Reserve Bank of St. Louis Review.
12. Ghysels, Eric & Santa-Clara, Pedro & Valkanov, Rossen, 2006. “Predicting volatility: getting the most out of return data sampled at different frequencies,” Journal of Econometrics, Elsevier, vol. 131(1-2).
13. Agus Purnomo, (2017), The Effect of Inflation on The Currency Exchange Rate Seen in The Islamic, Journal Ekonomi dan Peranakan Syariah, vol (8), no(1).